题目内容
设平面向量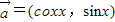 ,
,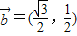 ,函数f(x)=
,函数f(x)=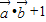 .求:
.求:①求函数f(x)的值域;
②求函数f(x)的单调增区间.
【答案】分析:①利用和差角公式f(x)可化为sin(x+ )+1,由正弦函数的有界性可得答案;
)+1,由正弦函数的有界性可得答案;
②令- +2kπ
+2kπ ,解出即可,注意表示形式;
,解出即可,注意表示形式;
解答:解:①依题意,f(x)=(cosx,sinx)•( ,
, )+1=
)+1= +1=sin(x+
+1=sin(x+ )+1,
)+1,
函数f(x)的值域为[0,2];
②令- +2kπ
+2kπ ,解得-
,解得- ,
,
所以函数f(x)的单调增区间为[- ](k∈Z).
](k∈Z).
点评:本题考查平面向量的数量积运算、正弦函数的单调性,属中档题.
 )+1,由正弦函数的有界性可得答案;
)+1,由正弦函数的有界性可得答案;②令-
 +2kπ
+2kπ ,解出即可,注意表示形式;
,解出即可,注意表示形式;解答:解:①依题意,f(x)=(cosx,sinx)•(
 ,
, )+1=
)+1= +1=sin(x+
+1=sin(x+ )+1,
)+1,函数f(x)的值域为[0,2];
②令-
 +2kπ
+2kπ ,解得-
,解得- ,
,所以函数f(x)的单调增区间为[-
 ](k∈Z).
](k∈Z).点评:本题考查平面向量的数量积运算、正弦函数的单调性,属中档题.

练习册系列答案
相关题目
 ,
, ,函数
,函数 .
. ,且
,且 时,求
时,求 的值.
的值. ,
, ,函数
,函数 .
. ,且
,且 时,求
时,求 的值.
的值.