题目内容
已知函数 .
.
(1)若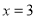 是
是 的极值点,求
的极值点,求 及
及 在
在 上的最大值;
上的最大值;
(2)若函数 是
是 上的单调递增函数,求实数
上的单调递增函数,求实数 的取值范围.
的取值范围.
(1) ,
, 在
在 上的最大值为15;
上的最大值为15;
(2)实数 的取值范围为:
的取值范围为: .
.
【解析】
试题分析:(1)先对函数求导,再把 代入导函数使之为0,即解得
代入导函数使之为0,即解得 的值,进一步可求
的值,进一步可求 ;令导函数为0,列表可求
;令导函数为0,列表可求 在
在 上的最大值;(2)函数
上的最大值;(2)函数 是
是 上的单调递增函数可转化为
上的单调递增函数可转化为 在R上恒成立,即可求出实数
在R上恒成立,即可求出实数 的取值范围.
的取值范围.
试题解析:(1) ,令
,令 ,即
,即 ∴
∴ .
.
∴ 4分
4分
令 ,解得
,解得 或
或 (舍去).
(舍去).
当 变化时,
变化时, ,
, ,的变化情况如下表:
,的变化情况如下表:
| 1 | (1,3) | 3 | (3,5) | 5 |
|
|
| 0 | + |
|
| 1 | 单调递减↘ | 9 | 单调递增↗ | 15 |
因此,当 时,
时, 在区间[1,5]上有最大值是
在区间[1,5]上有最大值是 . 8分
. 8分
(2)  是R上的单调递增函数转化为
是R上的单调递增函数转化为 在R上恒成立, 10分
在R上恒成立, 10分
从而有 ,由
,由 ,解得
,解得 12分
12分
考点:导函数的应用、恒成立问题、函数与方程思想.

练习册系列答案
相关题目