题目内容
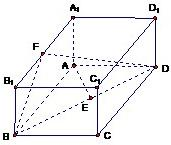
如图,已知长方体ABCD—A1B1C1D1中,AD=2,AB=4,AA1=6,E是AB的中点,过D1、C、E的平面交AA1于F.(I)求二面角D1—CE—D的正切值;
(II)求长方体被平面D1CEF截得的上、下两部分的体积之比.

答案:
解析:
解析:
| 答案:解:(I)连结D1E、DE,
∵E是AB的中点,∴BE=AE=2, ∴又BC=AD=2, ∴CE=DE=2 ∴CE⊥DE. 又∵D1D⊥平面ABC,∴CE⊥D1E,∴∠D1ED是二面角D1—CE—D的平面角, ∴ ∵平面C1D//平面AB1,∴EF//CD1. 又A1B//CD1, ∴EF//A1B. ∵E是AB的中点,∴F是AA1的中点. 由已知,长方体的体积等于48,而V2等于四棱锥D1—AECD与三棱锥D1—AEF的体积之和,而
|

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点. 如图,已知长方体ABCD-A1B1C1D1中,AB=
如图,已知长方体ABCD-A1B1C1D1中,AB= 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE. 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2 (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F