题目内容
定义运算min{x,y}= ,已知函数g(x)=min{(
,已知函数g(x)=min{( )x,2x+1},则g(x)的最大值为________.
)x,2x+1},则g(x)的最大值为________.
1
分析:由已知中 ,结合一次函数和指数函数的图象和性质可得g(x)=min{(
,结合一次函数和指数函数的图象和性质可得g(x)=min{( )x,2x+1}=
)x,2x+1}= ,进而分析出函数g(x)的单调性,可得g(x)的最大值.
,进而分析出函数g(x)的单调性,可得g(x)的最大值.
解答:∵
∴g(x)=min{( )x,2x+1}=
)x,2x+1}= ,
,
∴g(x)在(-∞,0]上为增函数,在[0,+∞)上为减函数
故当x=0时,函数g(x)取最大值为1
故答案为:1
点评:本题考查的知识点是函数最值的应用,其中熟练掌握基本初等函数的图象和性质,并真正理解新定义的含义是解答的关键.
分析:由已知中
 ,结合一次函数和指数函数的图象和性质可得g(x)=min{(
,结合一次函数和指数函数的图象和性质可得g(x)=min{( )x,2x+1}=
)x,2x+1}= ,进而分析出函数g(x)的单调性,可得g(x)的最大值.
,进而分析出函数g(x)的单调性,可得g(x)的最大值.解答:∵

∴g(x)=min{(
 )x,2x+1}=
)x,2x+1}= ,
,∴g(x)在(-∞,0]上为增函数,在[0,+∞)上为减函数
故当x=0时,函数g(x)取最大值为1
故答案为:1
点评:本题考查的知识点是函数最值的应用,其中熟练掌握基本初等函数的图象和性质,并真正理解新定义的含义是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
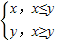 ,已知函数g(x)=min{(
,已知函数g(x)=min{( )x,2x+1},则g(x)的最大值为 .
)x,2x+1},则g(x)的最大值为 . ,已知函数g(x)=min{(
,已知函数g(x)=min{( )x,2x+1},则g(x)的最大值为 .
)x,2x+1},则g(x)的最大值为 . ,已知函数g(x)=min{(
,已知函数g(x)=min{( )x,2x+1},则g(x)的最大值为 .
)x,2x+1},则g(x)的最大值为 .