题目内容
已知奇函数f(x)在(-∞,0)∪(0,+∞)上有定义,在(0,+∞)上是增函数,f(1)=0,又知函数g(θ)=sin2θ+mcosθ-2m,θ∈[0,| π | 2 |
分析:利用奇函数在对称区间的单调性相同得到f(x)在(-∞,0)上也是增函数,f(-1)=0,将集合N中的0用f(-1)代替,利用f(x)的单调性将f脱去,利用三角函数的平方关系将正弦用余弦表示,通过换元转化为二次不等式恒成立,通过转化为求二次函数的最值,通过对对称轴的讨论求出最值.
解答:解:∵奇函数f(x)在(0,+∞)上是增函数,∴f(x)在(-∞,0)上也是增函数,
又由f(1)=0得f(-1)=-f(1)=0
∴满足
的条件是
即g(θ)<-1(θ∈[0,
]),即sin2θ+mcosθ-2m<-1,
也即-cos2θ+mcosθ-2m+2<0.
令t=cosθ,则t∈[0,1],又设δ(t)=-t2+mt-2m+2,0≤t≤1
要使δ(t)<0,必须使δ(t)在[0,1]内的最大值小于零
1°当
<0即m<0时,δ(t)max=δ(0)=-2m+2,解不等式组
知m∈∅
2°当0≤
≤1即0≤m≤2时,δ(t)max=
,
由
<0,解得4-2
≤m≤4+2
,故有2≥m≥4-2
当
>1即m>2时,δ(t)max=-m+1,解不等式组
得m>2
综上:M∩N={m|m>4-2
}
又由f(1)=0得f(-1)=-f(1)=0
∴满足
|
|
即g(θ)<-1(θ∈[0,
| π |
| 2 |
也即-cos2θ+mcosθ-2m+2<0.
令t=cosθ,则t∈[0,1],又设δ(t)=-t2+mt-2m+2,0≤t≤1
要使δ(t)<0,必须使δ(t)在[0,1]内的最大值小于零
1°当
| m |
| 2 |
|
2°当0≤
| m |
| 2 |
| m2-8m+8 |
| 4 |
由
| m2-8m+8 |
| 4 |
| 2 |
| 2 |
| 2? |
当
| m |
| 2 |
|
综上:M∩N={m|m>4-2
| 2 |
点评:本题考查奇函数在对称区间上的单调性相同、考查利用函数的单调性脱去对应法则将抽象不等式转化为具体不等式、考查换元法注意换元后新变量的范围、考查不等式恒成立转化为函数的最值、考查二次函数的最值取决于对称轴与区间的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知奇函数f(x)在[-1,0]上单调递减,又α,β为锐角三角形的两内角,则有( )
| A、f(sinα-sinβ)≥f(cosα-cosβ) | B、f(sinα-cosβ)>f(cosα-sinβ) | C、f(sinα-cosβ)≥f(cosα-sinβ) | D、f(sinα-cosβ)<f(cosα-sinβ) |
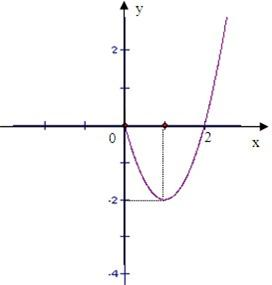 已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分,
已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分,