题目内容
命题“对所有的正数x,
>x-1”的否定是
| x |
存在正数x,
≤x-1
| x |
存在正数x,
≤x-1
.| x |
分析:根据命题:对所有的正数x,
>x-1为全称命题,其否定形式为特称命题,由“所有”否定为“存在”,“>“的否定为“≤”可得答案.
| x |
解答:解:∵命题:对所有的正数x,
>x-1为全称命题,
∴命题P的否定形式为:存在正数x,
≤x-1.
故答案为:存在正数x,
≤x-1.
| x |
∴命题P的否定形式为:存在正数x,
| x |
故答案为:存在正数x,
| x |
点评:此题是基础题.本题主要考查全称命题与特称命题的相互转化问题.这里注意,全称命题的否定是特称命题,反过来特称命题的否定是全称命题.

练习册系列答案
相关题目
 >x-1
>x-1 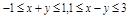 ,则
,则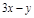 的范围是
的范围是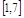 ;
;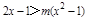 对满足
对满足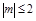 的所有m都成立,则x的范围是
的所有m都成立,则x的范围是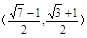 ;
;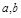 满足
满足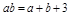 ,则
,则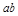 的取值范围是
的取值范围是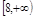
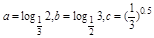 大小关系是
大小关系是
 ”的否定是________.
”的否定是________.