题目内容
若1,3为函数f(x)=
x3+bx2+cx(b,c∈R)的两个极值点,则曲线y=f(x)在点(-1,f(-1))处的切线的斜率为( )
| 1 |
| 3 |
分析:先根据极值点必定是导函数对应方程的根建立方程组,求出b与c的值,再根据导数的几何意义即在某点处的导数即该点处切线的斜率,将-1代入导函数即可求出所求.
解答:解:∵f(x)=
x3+bx2+cx,
∴f′(x)=x2+2bx+c,
∵1,3为函数f(x)=
x3+bx2+cx(b,c∈R)的两个极值点,
∴
,
解得
,
即f′(x)=x2-4x+3,
∴f′(-1)=(-1)2-4×(-1)+3=8,
即曲线y=f(x)在点(-1,f(-1))处的切线的斜率为8.
故选A.
| 1 |
| 3 |
∴f′(x)=x2+2bx+c,
∵1,3为函数f(x)=
| 1 |
| 3 |
∴
|
解得
|
即f′(x)=x2-4x+3,
∴f′(-1)=(-1)2-4×(-1)+3=8,
即曲线y=f(x)在点(-1,f(-1))处的切线的斜率为8.
故选A.
点评:本题考查了导数的几何意义,利用导数研究函数的极值,解题时要注意运用极值点必定是导函数对应方程的根,导数的几何意义即在某点处的导数即该点处切线的斜率,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
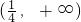 上为减函数;
上为减函数;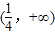 上为减函数;
上为减函数;