题目内容
已知偶函数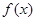
在区间
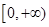单调递增，
则满足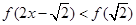
的
取值
范围是（ ）
A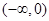． | B． |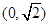
C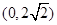． | D． |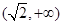
B
解析考点：奇偶性与单调性的综合．
分析：由f（x）是偶函数，得f（2x-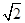 
）=f（|2x- 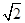|），又f（x）在[0，+∞）上递增，得f(2x- 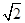)＜f(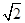)?|2x- 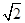|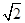＜，从而可解出x的范围．
解：由题意得：f(2x-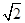)＜f()?f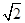（|2x-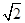|）＜f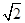（）?|2x-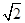|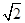＜，解得0＜x＜．
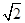故x的取值范围为：（0，）．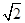
选B。
练习册系列答案
阅读快车系列答案
相关题目
函数
的定义域为
A．  | B． | C． | D． |
函数f(x)＝log2x－x＋2的零点个数为( )
| A．0 | B．1 |
| C．2 | D．3 |
．函数 
, 
[0,3]的值域为（ ）
| A．[0,3] | B．[1,3] | C．[-1,0] | D．[-1,3] |
若函数
在区间
内是减函数，则实数
的取值范围是
A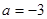． | B． | C． | D．以上都不对 |
已知函数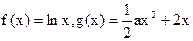
,若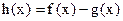
存在单调减区间,则实数
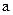的取值范围是( )
A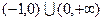． | B．(0,1) | C．(-1,0) | D． |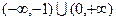
线段y= l，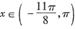
与函数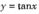
，
，
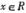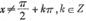图象的交点个数是
| A．1 | B．2 | C．3 | D．4 |
设函数f（x）（x∈R）为奇函数，f（1）＝
，
f（x＋2）＝f（x）＋f（2），则f（5）＝
| A．0 | B．1 | C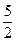． | D．5 |
设实数、y满足约束条件，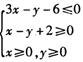
，若目标函数
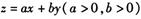的最大值为12,则
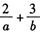的最小值为（）
| A．4 | B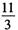． | C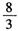． | D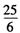． |