题目内容
某工厂有一段旧墙长14m,现准备利用这段旧墙为一面建造平面图形为矩形,面积为126m2的厂房,工程条件是:①建1m新墙的费用为a元;=2 ②修1m旧墙的费用为| a |
| 4 |
| a |
| 2 |
(1)利用旧墙一段x m(0<x<14)为矩形一边;
(2)矩形厂房利用旧墙的一面边长x≥14;
问如何利用旧墙建墙费用最省?试比较(1)(2)两种方案哪个更好.
分析:根据题意将实际问题的数学模型建立起来是解决本题的关键.利用两种不同的方案分别给出费用的表达式,通过比较大小确定出哪个方案更好.
解答:解:(1)方案:修旧墙费用为x•
元,拆旧墙造新墙费用为(14-x)•
,
其余新墙费用:(2x+
-14)a
∴总费用y=7a(
+
-1)(0<x<14)
∴y=7a(
-
)2+35a≥35a,当x=12时,ymin=35a;
(2)方案,利用旧墙费用为14•
=
(元),建新墙费用为(2x+
-14)a(元)
总费用为:y=2a(x+
)-
a(x≥14)
设f(x)=x+
(x≥14),则f′(x)=1-
=
,
当x≥14时,f'(x)>0,f(x)为增函数,∴f(x)min=f(14)=35.5a.
由35a<35.5a知,采用(1)方案更好些.
答:采用(1)方案更好些.
| a |
| 4 |
| a |
| 2 |
其余新墙费用:(2x+
| 2×126 |
| x |
∴总费用y=7a(
| x |
| 4 |
| 36 |
| x |
∴y=7a(
| ||
| 2 |
| 6 | ||
|
(2)方案,利用旧墙费用为14•
| a |
| 4 |
| 7a |
| 2 |
| 252 |
| x |
总费用为:y=2a(x+
| 126 |
| x |
| 21 |
| 2 |
设f(x)=x+
| 126 |
| x |
| 126 |
| x2 |
| x2-126 |
| x2 |
当x≥14时,f'(x)>0,f(x)为增函数,∴f(x)min=f(14)=35.5a.
由35a<35.5a知,采用(1)方案更好些.
答:采用(1)方案更好些.
点评:本题考查函数模型的应用问题,考查建立函数模型解决实际问题的意识,通过建立的模型选择合适的方法求解相应的最值,通过最值之间的关系比较进行选择.突出数学的应用价值.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 元;(3) 拆去1m的旧墙,用可得的建材建1m的新墙的费用为
元;(3) 拆去1m的旧墙,用可得的建材建1m的新墙的费用为 元,经讨论有两种方案:
元,经讨论有两种方案: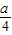 元;=3 ③拆去1m的旧墙,用可得的建材建1m的新墙的费用为
元;=3 ③拆去1m的旧墙,用可得的建材建1m的新墙的费用为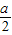 元,经讨论有两种方案:
元,经讨论有两种方案: