Question

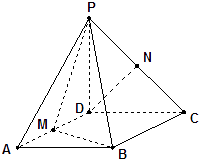
【题目】如图，在△ABC中， ，
（1）用 ， 表示 ；
（2）若 ， ，求证： ；
（3）若 ，求 的值．

Answer 1

【答案】
（1）解：因为 ，所以 ，

所以 ，

（2）证明：因为 ，所以 ，即 ，

即 ，又因为 ，

所以 ，即 ．

所以 ，所以 ，

（3）解：因为 ，所以 ，

即 ，因此 ，

同理 ，又 ，所以 ，

因为 ，所以 ，

即 ①

又因为 ， ，所以 ，所以 ，

即 ②

由①②得 ．

【解析】（1）根据向量的加减的几何意义即可求出，（2）根据向量的模和向量的垂直的条件即可判断，（3）根据向量的加减的几何意义和向量的数量积的运算即可求出
【考点精析】利用平面向量的基本定理及其意义对题目进行判断即可得到答案，需要熟知如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使．