题目内容
如图，在等腰梯形ABCD中，上底CD=3，下底AB=4，E、F分别为AB、CD中点，分别沿DE、CE把△ADE与△BCE折起，使A、B重合于点P．
（1）求证：PE⊥CD；
（2）若点P在面CDE的射影恰好是点F，求EF的长．
（1）证明：连接PF，∵F、E分别是等腰梯形上、下两底的中点，∴EF⊥CD．
又∵AD=BC，即PD=PC且F为CD的中点，∴PF⊥CD．
又EF，PF?面PEF，EF∩PF=F，∴CD⊥面PEF．
又PE?面PEF，∴PE⊥CD．
（2）解：若点P在面CDE的射影恰好是点F，即PF⊥面CDE于F，EF?面CDE，所以，PF⊥EF
设EF=x，由已知EF为等腰梯形的高，且PE⊥CF
∵PE=BE=
AB=2，∴PF=
∵CF=CD=
，∴PC=
=
在等腰梯形ABCD中，BC=
=
∵PC=BC，∴=，∴x=
，
∴EF的长为．
分析：（1）连接PF，证明CD⊥面PEF，利用线面垂直的性质，可得PE⊥CD；
（2）证明PF⊥面CDE于F，可得PF⊥EF，分别计算PC，BC，利用PC=BC，即可求EF的长．
点评：本题考查线面垂直、线线垂直，考查学生的计算能力，考查学生分析解决问题的能力，属于中档题．
又∵AD=BC，即PD=PC且F为CD的中点，∴PF⊥CD．
又EF，PF?面PEF，EF∩PF=F，∴CD⊥面PEF．
又PE?面PEF，∴PE⊥CD．
（2）解：若点P在面CDE的射影恰好是点F，即PF⊥面CDE于F，EF?面CDE，所以，PF⊥EF
设EF=x，由已知EF为等腰梯形的高，且PE⊥CF
∵PE=BE=
AB=2，∴PF=∵CF=
CD=，∴PC==在等腰梯形ABCD中，BC=
=∵PC=BC，∴
=，∴x=，∴EF的长为
．分析：（1）连接PF，证明CD⊥面PEF，利用线面垂直的性质，可得PE⊥CD；
（2）证明PF⊥面CDE于F，可得PF⊥EF，分别计算PC，BC，利用PC=BC，即可求EF的长．
点评：本题考查线面垂直、线线垂直，考查学生的计算能力，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
步步高达标卷系列答案
相关题目
如图，在等腰梯形ABCD中，AB∥DC，AB=4，CD=2，等腰梯形的高为3，O为AB中点，PO⊥平面ABCD，垂足为O，PO=2，EA∥PO．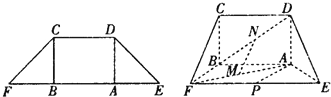
如图，在等腰梯形CDEF中，CB、DA是梯形的高，AE=BF=2，AB=2
选修4-1；几何证明选讲．
（2012•河北模拟）如图，在等腰梯形ABCD中，CD=2，AB=4，AD=BC=