题目内容
 已知公差不为零的等差数列{an}的前n项和为Sn,点(n,Sn)都在二次函数y=f(x)的图象上(如图).已知函数y=f(x)的图象的对称轴方程是x=
已知公差不为零的等差数列{an}的前n项和为Sn,点(n,Sn)都在二次函数y=f(x)的图象上(如图).已知函数y=f(x)的图象的对称轴方程是x= .若点(n,an)在函数y=g(x)的图象上,则函数y=g(x)的图象可能是
.若点(n,an)在函数y=g(x)的图象上,则函数y=g(x)的图象可能是
- A.

- B.

- C.

- D.

B
分析:设公差不为零的等差数列{an}的通项an=an+b(a≠0)可得g(x)=ax+b,Sn ═ n2+(b+
n2+(b+ )n,即f(x)=
)n,即f(x)= x2+(b+
x2+(b+ )x,结合图象可得a<0,-
)x,结合图象可得a<0,- =
= .化简可得 a<0,b=-2a>0,由此可得直线g(x)=ax+b 在坐标系中的位置.
.化简可得 a<0,b=-2a>0,由此可得直线g(x)=ax+b 在坐标系中的位置.
解答:设公差不为零的等差数列{an}的通项an=an+b(a≠0),则 y=g(x)=ax+b,Sn = =
= n2+(b+
n2+(b+ )n.
)n.
再由点(n,Sn)都在二次函数y=f(x)的图象上可得 f(x)= x2+(b+
x2+(b+ )x.
)x.
结合图象可得a<0,- =
= .
.
化简可得 a<0,b=-2a>0,即直线g(x)=ax+b 的斜率小于0,在y轴上的截距大于0,
故选B.
点评:本题主要考查等差数列与一次函数的关系,等差数列的通项公式,等差数列的前n项和公式的应用,体现了数形结合的数学思想,属于基础题.
分析:设公差不为零的等差数列{an}的通项an=an+b(a≠0)可得g(x)=ax+b,Sn ═
 n2+(b+
n2+(b+ )n,即f(x)=
)n,即f(x)= x2+(b+
x2+(b+ )x,结合图象可得a<0,-
)x,结合图象可得a<0,- =
= .化简可得 a<0,b=-2a>0,由此可得直线g(x)=ax+b 在坐标系中的位置.
.化简可得 a<0,b=-2a>0,由此可得直线g(x)=ax+b 在坐标系中的位置.解答:设公差不为零的等差数列{an}的通项an=an+b(a≠0),则 y=g(x)=ax+b,Sn =
 =
= n2+(b+
n2+(b+ )n.
)n.再由点(n,Sn)都在二次函数y=f(x)的图象上可得 f(x)=
 x2+(b+
x2+(b+ )x.
)x.结合图象可得a<0,-
 =
= .
.化简可得 a<0,b=-2a>0,即直线g(x)=ax+b 的斜率小于0,在y轴上的截距大于0,
故选B.
点评:本题主要考查等差数列与一次函数的关系,等差数列的通项公式,等差数列的前n项和公式的应用,体现了数形结合的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
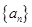 与公比为
与公比为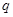 的等比数列
的等比数列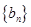 有相同的首项,同时满足
有相同的首项,同时满足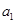 ,
,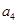 ,
,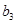 成等比,
成等比, ,
,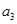 ,
,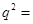 ( )
( )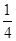 B.
B.
 C.
C.
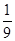 D.
D.