题目内容
8、若A?B,A?C,B={0,1,2,3},C={0,2,4,8},则满足上述条件的集合A为
Φ,{0},{2},{0,2}
.分析:根据A?B,A?C,得到A⊆(B∩C),由B={0,1,2,3},C={0,2,4,8},求出B∩C并写出它的所有子集,即是满足上述条件的集合A的所有情况.
解答:解:∵A?B,A?C,
∴A⊆(B∩C),
∵B={0,1,2,3},C={0,2,4,8},
∴B∩C={0,2},
∴A=Φ,{0},{2},{0,2}.
故答案为Φ,{0},{2},{0,2}.
∴A⊆(B∩C),
∵B={0,1,2,3},C={0,2,4,8},
∴B∩C={0,2},
∴A=Φ,{0},{2},{0,2}.
故答案为Φ,{0},{2},{0,2}.
点评:此题是个基础题.考查集合的包含关系判断及应用,以及灵活应用知识分析、解决问题的能力.

练习册系列答案
相关题目
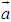 ,
,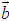 ,
,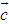 ,若
,若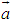 ∥
∥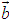 ,
,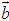 ∥
∥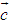 则
则 ∥
∥