题目内容
（本小题满分12分）
已知函数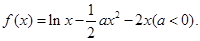
(1)若函数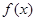
在定义域内单调递增，求
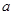的取值范围；
（2)若
且关于x的方程
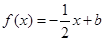在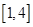
上恰有两个不相等的实数根，求实数
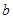的取值范围；
(3)设各项为正的数列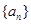
满足：
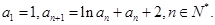求证：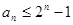
【答案】
（1）
（2）
（3）证明略
【解析】
解：（1）
依题意
在
时恒成立，即
在恒成立.
则
在恒成立，
即
当
时，
取最小值
∴
的取值范围是
……
（2）
设
则
列表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
极大值 |
¯ |
极小值 |
|
∴
极小值
，极大值
，
又
……
方程
在[1，4]上恰有两个不相等的实数根.
则
， 得 …………
（3）设
，则
在
为减函数，且
故当
时有
.
假设
则
，故
从而
即
，∴
…………
练习册系列答案
阳光课堂课时作业系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
