题目内容
 (k>1)所表示的平面区域为D,若D的面积为S,则
(k>1)所表示的平面区域为D,若D的面积为S,则 的最小值为
的最小值为
- A.24
- B.30
- C.32
- D.64
C
分析:由题意推出约束条件表示的可行域,是一个直角三角形,求出y=-kx+4k在两坐标轴上的截距,求出区域的面积,代入表达式,然后换元,利用基本不等式求出最值.
解答:由不等式组可知围成的平面区域为直角三角形
分别将x=0,y=0代入方程y=-kx+4k
可知三角形面积S=
将S=8k代入 得
得 
令k-1=t∈(0,+∞)
原式=8t+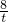 +16≥32
+16≥32
所以 最小值为32
最小值为32
故答案为:32.
点评:本题考查简单的线性规划,基本不等式,换元法等知识,是中档题.
分析:由题意推出约束条件表示的可行域,是一个直角三角形,求出y=-kx+4k在两坐标轴上的截距,求出区域的面积,代入表达式,然后换元,利用基本不等式求出最值.
解答:由不等式组可知围成的平面区域为直角三角形
分别将x=0,y=0代入方程y=-kx+4k
可知三角形面积S=

将S=8k代入
 得
得 
令k-1=t∈(0,+∞)
原式=8t+
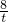 +16≥32
+16≥32所以
 最小值为32
最小值为32故答案为:32.
点评:本题考查简单的线性规划,基本不等式,换元法等知识,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目