题目内容

设椭圆 $数学公式$ （a＞b＞0）的两焦点为F₁、F₂，若椭圆上存在一点Q，使∠F₁QF₂=120°，椭圆离心率e的取值范围为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

A
分析：依题意，椭圆的焦点在x轴上，设椭圆的上顶点为A，由∠F₁AO≥60°，即可求得它的离心率的取值范围．
解答：椭圆的焦点在x轴，设椭圆的上顶点为A，
∵椭圆上存在一点Q，∠F₁QF₂=120°，
∴∠F₁AO≥60°，
∴tan∠F₁AO= $\text{[math]}$ ≥ $\text{[math]}$ ，
∴ $\text{[math]}$ ≤ $\text{[math]}$ ? $\text{[math]}$ = $\text{[math]}$ ≤ $\text{[math]}$ ，
∴ $\text{[math]}$ ≥ $\text{[math]}$ ，
∴e= $\text{[math]}$ ≥ $\text{[math]}$ ，又e＜1．
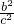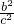∴ $\text{[math]}$ ≤e＜1．
故选A．
点评：本题考查椭圆的简单性质，求得∠F₁AO≥60°是关键，也是难点，考查分析与逻辑思维能力，属于难题．

练习册系列答案

金版卷王课程探究大试卷系列答案

金榜之路系列答案

金点中考系列答案

金海全A突破系列答案

金考卷45套汇编系列答案

全景文化中考试题汇编3年真题2年模拟系列答案

金牌教练赢在燕赵系列答案

0系列答案

金题金卷热点测试系列答案

金钥匙试卷系列答案

相关题目

在直角坐标系xOy中,设椭圆C:(a＞b＞0)的左、右两个焦点分别为F₁、F₂.过右焦点F₂且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(,1).

(1)求椭圆C的方程;

(2)设椭圆C的一个顶点为B(0,-b),直线BF₂交椭圆C于另一点N,求△F₁BN的面积.

设椭圆+=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.

(1)求椭圆的离心率e;

(2)设直线PF2与椭圆相交于A,B两点.若直线PF2与圆(x+1)2+(y-)2=16相交于M,N两点,且|MN|=|AB|,求椭圆的方程.

设椭圆+=1(a>b>0)的左焦点为F,离心率为,过点F且与x轴垂直的直线被椭圆截得的线段长为.

(1)求椭圆的方程;

(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若·+·=8,求k的值.

设椭圆C:(“a>b〉0)的左焦点为，椭圆过点P（)

(1)求椭圆C的方程；

(2)已知点D(1, 0),直线l:与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形，求k的取值范围.

设椭圆+=1(a＞b＞0)的左焦点为F₁(－2,0),左准线l₁与x轴交于点N(－3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.

(1)求直线l和椭圆的方程；

(2)求证:点F₁(－2,0)在以线段AB为直径的圆上.