题目内容
已知矩阵A=![]() ,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3).(1)求实数a的值;
,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3).(1)求实数a的值;
(2)求矩阵A的特征值及特征向量.
(1)-4(2)矩阵A的属于特征值3的一个特征向量为![]() .矩阵A的属于特征值-1的一个特征向量为
.矩阵A的属于特征值-1的一个特征向量为![]() .
.
解析:
(1)由![]()
![]() =
=![]()
得a+1=-3![]() a=-4.
a=-4.
(2)由(1)知A=![]()
则矩阵A的特征多项式为
f(![]() )=
)=![]() =(
=(![]() -1)2-4=
-1)2-4=![]() 2-2
2-2![]() -3
-3
令f(![]() )=0,得矩阵A的特征值为-1或3.
)=0,得矩阵A的特征值为-1或3.
设矩阵A的特征向量为![]()
当![]() =-1时,
=-1时,![]()
![]() =(-1)
=(-1) ![]()
即![]() ,所以y=2x.
,所以y=2x.
∴矩阵A的属于特征值-1的一个特征向量为![]() .
.
当![]() =3时,
=3时,![]()
![]() =3
=3![]() ,
,
即![]() ,所以2x+y=0.
,所以2x+y=0.
∴矩阵A的属于特征值3的一个特征向量为![]() .
.

练习册系列答案
相关题目
 ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的值;
的值; 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于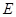 .
. 的长.
的长. ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
,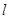 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
的最小值; ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的值;
的值; 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以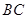 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长. ,其中
,其中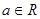 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
, 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
的最小值;