题目内容
记实数x1,x2,…,xn中的最大数为max{x1,x2,…,xn},最小数为min{x1,x2,…,xn}.设△ABC的三边边长分别为a,b,c,且a≤b≤c,定义△ABC的倾斜度为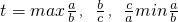 ,
,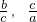 .
.
(ⅰ)若△ABC为等腰三角形,则t=________;
(ⅱ)设a=1,则t的取值范围是________.
1 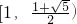
分析:(i)分三种a=b=c、a=b<c和a<b=c三种情况加以讨论,分别求出max{ }和min{
}和min{ }的值,即可算出总有实数t=1成立,得到本题答案;
}的值,即可算出总有实数t=1成立,得到本题答案;
(ii)根据题意,可得max{ }=c且min{
}=c且min{ }=
}=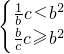 ,因此对c<b2和c≥b2两种情况加以讨论,利用三角形两边之和大于第三边和不等式的性质进行推导,联解不等式组可得t的取值范围是[1,
,因此对c<b2和c≥b2两种情况加以讨论,利用三角形两边之和大于第三边和不等式的性质进行推导,联解不等式组可得t的取值范围是[1, ).
).
解答:(i)若a=b=c,则max{ }=min{
}=min{ }=1
}=1
∴t=max{ }•min{
}•min{ }=1;
}=1;
若a=b<c,则max{ }=
}= ,min{
,min{ }=
}=
∴t=max{ }•min{
}•min{ }=
}= •
• =
= =1;
=1;
若a<b=c,则max{ }=
}= ,min{
,min{ }=
}=
∴t=max{ }•min{
}•min{ }=
}= •
• =
= =1
=1
综上所述,可得若△ABC为等腰三角形,则t=1;
(ii)∵a=1,a≤b≤c,
∴max{ }=max{
}=max{ ,
, ,c}=c
,c}=c
而min{ }=min{
}=min{ ,
, ,c}=
,c}=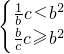
①当c<b2时,t=c• =
= ,可得c=tb,(t≥1)
,可得c=tb,(t≥1)
∵由1+b>c,得1+b>tb,∴t≠1时,b<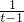
∵c=tb<b2,∴t<b,可得t<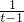 ,解之得1<t<
,解之得1<t<
而t=1时,b=c>a=1,符合题意.所以此时t的范围为[1, )
)
②当c≥b2时,t=c• =b,可得
=b,可得
∵1+b>c且c≥b2,
∴1+b>b2,解之得1≤b<
即1≤t< ,得此时t的范围为[1,
,得此时t的范围为[1, )
)
综上所述,可得当a=1时,t的取值范围是[1, ).
).
故答案为:1,[1, )
)
点评:本题给出三角形三边中任意两边的比值,求它们的最大值与最小值之积的取值范围,着重考查了函数最值的意义、三角形两边之和大于第三边、不等式的基本性质和不等式的解法等知识,属于中档题.
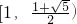
分析:(i)分三种a=b=c、a=b<c和a<b=c三种情况加以讨论,分别求出max{
 }和min{
}和min{ }的值,即可算出总有实数t=1成立,得到本题答案;
}的值,即可算出总有实数t=1成立,得到本题答案;(ii)根据题意,可得max{
 }=c且min{
}=c且min{ }=
}=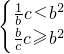 ,因此对c<b2和c≥b2两种情况加以讨论,利用三角形两边之和大于第三边和不等式的性质进行推导,联解不等式组可得t的取值范围是[1,
,因此对c<b2和c≥b2两种情况加以讨论,利用三角形两边之和大于第三边和不等式的性质进行推导,联解不等式组可得t的取值范围是[1, ).
).解答:(i)若a=b=c,则max{
 }=min{
}=min{ }=1
}=1∴t=max{
 }•min{
}•min{ }=1;
}=1;若a=b<c,则max{
 }=
}= ,min{
,min{ }=
}=
∴t=max{
 }•min{
}•min{ }=
}= •
• =
= =1;
=1;若a<b=c,则max{
 }=
}= ,min{
,min{ }=
}=
∴t=max{
 }•min{
}•min{ }=
}= •
• =
= =1
=1综上所述,可得若△ABC为等腰三角形,则t=1;
(ii)∵a=1,a≤b≤c,
∴max{
 }=max{
}=max{ ,
, ,c}=c
,c}=c而min{
 }=min{
}=min{ ,
, ,c}=
,c}=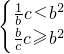
①当c<b2时,t=c•
 =
= ,可得c=tb,(t≥1)
,可得c=tb,(t≥1)∵由1+b>c,得1+b>tb,∴t≠1时,b<
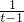
∵c=tb<b2,∴t<b,可得t<
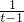 ,解之得1<t<
,解之得1<t<
而t=1时,b=c>a=1,符合题意.所以此时t的范围为[1,
 )
)②当c≥b2时,t=c•
 =b,可得
=b,可得∵1+b>c且c≥b2,
∴1+b>b2,解之得1≤b<

即1≤t<
 ,得此时t的范围为[1,
,得此时t的范围为[1, )
)综上所述,可得当a=1时,t的取值范围是[1,
 ).
).故答案为:1,[1,
 )
)点评:本题给出三角形三边中任意两边的比值,求它们的最大值与最小值之积的取值范围,着重考查了函数最值的意义、三角形两边之和大于第三边、不等式的基本性质和不等式的解法等知识,属于中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
记实数x1,x2,…xn中的最大数为max{x1,x2,…xn},最小数为min{x1,x2,…xn}.已知△ABC的三边边长为a、b、c(a≤b≤c),定义它的倾斜度为t=max{
,
,
}•min{
,
,
},x,则“t=1”是“△ABC为等边三角形”的( )
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| b |
| c |
| c |
| a |
| A、充分布不必要的条件 |
| B、必要而不充分的条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
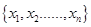 ,最小数为
,最小数为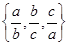 ·min
·min