题目内容
已知函数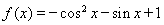 .
.
(Ⅰ)求函数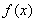 的最小值;
的最小值;
(Ⅱ)若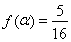 ,求
,求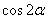 的值.
的值.
【答案】
(Ⅰ)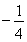 (Ⅱ)
(Ⅱ)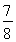
【解析】
试题分析:(Ⅰ)将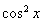 用同角三角函数关系式转化为
用同角三角函数关系式转化为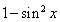 ,此函数及转化为关于
,此函数及转化为关于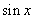 的二次函数,将三角函数最值问题转化为二次函数配方法求最值问题。根据正弦函数范围为
的二次函数,将三角函数最值问题转化为二次函数配方法求最值问题。根据正弦函数范围为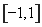 ,即可求出
,即可求出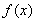 的最小值。(Ⅱ)当
的最小值。(Ⅱ)当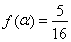 时,可计算求得
时,可计算求得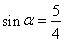 或
或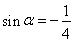 ,因为
,因为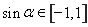 ,所以
,所以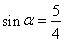 舍掉,将
舍掉,将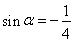 代入余弦二倍角公式
代入余弦二倍角公式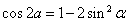 ,即可求得
,即可求得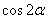 的值。
的值。
试题解析:解:(Ⅰ)因为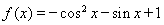
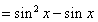
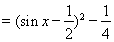 ,
,
又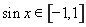 ,所以当
,所以当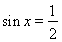 时,函数
时,函数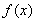 的最小值为
的最小值为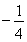 .…… 6分
.…… 6分
(Ⅱ)由(Ⅰ)得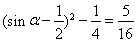 ,
,
所以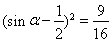 .
.
于是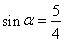 (舍)或
(舍)或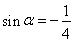 .
.
又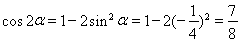 . 13分
. 13分
考点:1三角函数同角三角函数关系式,二倍角公式;2正弦函数值域;3二次函数最值问题。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数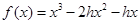 ,若
,若 且
且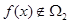 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得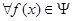 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


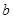
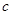




 ,编写一个程序求函数值.
,编写一个程序求函数值. 试画出求函数值的程序框图.
试画出求函数值的程序框图.