Question

在5×5的棋盘中，放入3颗黑子和2颗白子，它们均不在同一行且不在同一列，则不同的排列方法种数为( )

A．150 B．200 C．600 D．1200

 

Answer 1

【答案】

D

【解析】

试题分析：如图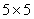的棋盘中，

黑
		黑
	白
			黑
				白

首先放入三颗黑子，在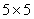的棋盘中，选出三行三列，共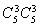种方法，然后放入三颗黑子，每一行放一颗黑子，共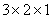种方法，然后在剩下的两行两列放两颗白子，共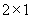种方法，所以不同的方法种数为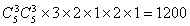种方法.故选D.

考点：1.分步计数原理；2.排列组合的综合应用.