题目内容
如果我们把形如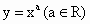 的函数成为幂函数,现已知幂函数
的函数成为幂函数,现已知幂函数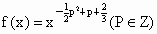 在(0,+∞)上是增函数,且在其定义域内是偶函数.
在(0,+∞)上是增函数,且在其定义域内是偶函数.
(1)求p的值,并写出相应的函数f(x);
(2)对于(1)中求得的函数f(x),设函数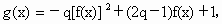 问是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在(-4,0)上是增函数?若存在,请求出q来,若不存在,请说明理由.
问是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在(-4,0)上是增函数?若存在,请求出q来,若不存在,请说明理由.
答案:略
解析:
解析:
|
∵ (1)f(x)在(0,+∞)是增函数,∴  . .
解得过且过- 1<p<3.由P∈Z,得P=0,1,2.当 P=0,或P=2时, 不合题意. 不合题意.
由此可知当 P=1时,相应的函数式为 . .
(2) 函数 .假设存在实数q(q<0)使得g(x)满足条件. .假设存在实数q(q<0)使得g(x)满足条件.
设  ,则 ,则 , ,
x ∈(-∞,-4)时,t∈[16,+∞), 为减函数. 为减函数.
x ∈(-4,0)时,t∈[0,16), .为减函数. .为减函数.
又由题意可知, t∈[16,+∞),g(t)为增函数,t ∈[16,+∞),g(t)为减函数,∴  为对称轴,∴ 为对称轴,∴ . . |

练习册系列答案
相关题目
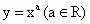 的函数成为幂函数,现已知幂函数
的函数成为幂函数,现已知幂函数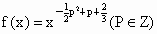 在(0,+∞)上是增函数,且在其定义域内是偶函数.
在(0,+∞)上是增函数,且在其定义域内是偶函数.
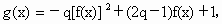 问是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在(-4,0)上是增函数?若存在,请求出q来,若不存在,请说明理由.
问是否存在实数q(q<0),使得g(x)在区间(-∞,-4]上是减函数,且在(-4,0)上是增函数?若存在,请求出q来,若不存在,请说明理由.