Question

（本小题满分12分）

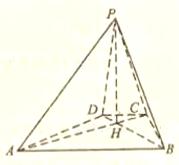
如图，已知四棱锥的底面为等腰梯形，∥,,垂足为，是四棱锥的高。

（Ⅰ）证明：平面 平面；

（Ⅱ）若,60°,求四棱锥的体积。

 

Answer 1

解：

          （Ⅰ）因为PH是四棱锥P-ABCD的高。

           所以ACPH,又ACBD,PH,BD都在平面PBD内,且PHBD=H.

           所以AC平面PBD.

           故平面PAC平面PBD.                             ……..6分

         （Ⅱ）因为ABCD为等腰梯形，AB∥CD,ACBD,AB=.

           所以HA=HB=.

           因为APB=ADB=60⁰

                所以PA=PB=,HD=HC=1.

          可得PH=.

          等腰梯形ABCD的面积为S=AC x BD = 2+.      ……..9分

          所以四棱锥的体积为V=x（2+）x=   ……..12分