题目内容
从学号为1~50的高一某班50名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是
| A.1,2,3,4,5 | B.5,15,25,35,45 | C.2,4,6,8,10 | D.4,13,22,31,40 |
B
解析试题分析:解:从学号为0~50的高一某班50名学生中随机选取5名同学参加数学测试,采用系统抽样间隔应为  =10,只有A答案中的编号间隔为10,故选B
=10,只有A答案中的编号间隔为10,故选B
考点:系统抽样
点评:本题主要考查了系统抽样方法.一般地,要从容量为N的总体中抽取容量为n的样本,可将总体分成均衡的若干部分,然后按照预先制定的规则,从每一部分抽取一个个体,得到所需要的样本

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
.以下茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)
| 甲组 | | 乙组 | |||
| | 9 | 0 | 9 | | |
 | 2 | 1 | 5 |  | 8 |
| 7 | 4 | 2 | 4 | | |
 ,乙组数据的平均数为
,乙组数据的平均数为 ,则
,则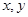 的值分别为 ( )
的值分别为 ( )A.
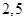 B.
B. C.
C. D.
D.
下列关于由最小二乘法求出的回归直线方程 =2-x的说法中,不正确的是
=2-x的说法中,不正确的是
| A.变量x与y正相关 |
B.该回归直线必过样本点中心( ) ) |
| C.当x=l时,y的预报值为l |
D.当残差平方和 越小时模型拟合的效果越好 越小时模型拟合的效果越好 |
为了评价某个电视栏目的改革效果,在改革前后分别从某居民点抽取了1000位居民进行调查,经过计算得K2 4.358,根据这一数据分析,下列说法正确的是( )
4.358,根据这一数据分析,下列说法正确的是( )
| A.有95%的人认为该栏日优秀 |
| B.有95%的人认为该栏目是否优秀与改革有关系 |
| C.有95%的把握认为电视栏目是否优秀与改革有关系 |
| D.没有理由认为电视栏目是否优秀与改革有关系 |
对具有线性相关关系的的变量 ,
, ,测得一组数据如下表
,测得一组数据如下表
 | 2 | 4 | 5 | 6 | 8 |
 | 20 | 40 | 60 | 70 | 80 |
 ,据此模型来预测当
,据此模型来预测当 时,
时, 的估计值为 ( )
的估计值为 ( )A.210 B.210.5 C.211.5 D.212.5
2012年学期末,某学校对100间学生公寓进行综合评比,依考核分数分为A,B,C,D四种等级,其中分数在 为D等级,有15间;分数在
为D等级,有15间;分数在 为C等级,有40间;分数在
为C等级,有40间;分数在 为B等级,有20间;分数在
为B等级,有20间;分数在 为D等级,有25间. 考核评估后,得其频率直方图如图所示,估计这100间学生公寓评估得分的中位数是
为D等级,有25间. 考核评估后,得其频率直方图如图所示,估计这100间学生公寓评估得分的中位数是
| A.78.65 | B.78.75 | C.78.80 | D.78.85 |
利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X和Y有关系”的可信度。如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为( )
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
以下有关线性回归分析的说法不正确的是( )
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使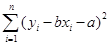 最小的a,b的值 最小的a,b的值 |
| C.相关系数r越小,表明两个变量相关性越弱 |
D. 越接近1,表明回归的效果越好 越接近1,表明回归的效果越好 |


 的值为( )
的值为( )