题目内容
已知直线l过原点,抛物线C的顶点在原点,焦点在x轴的正半轴上,且点A(-1,0)和点B(0,8)关于直线l的对称点都在C上,求直线l和抛物线C的方程.
思路分析:设∠B′Ox=α,利用对称的几何性质和三角函数知识求解.
解:设点A、B关于l的对称点为A′(x1,y1)、B′(x2,y2),
又设∠B′Ox=α,依题意,有|OA′|=|OA|=1,|OB′|=|OB|=8.
故x2=8cosα,y2=8sinα.
由∠BOA=90°,知∠B′OA′=90°.∴x1=cos(α-90°)=sinα,y1=sin(α-90°)=-cosα.
又x1>0,x2>0,故α为第一象限的角.∴A′(sinα,-cosα)、B′(8cosα,8sinα).
将A′、B′的坐标代入抛物线方程,得cos2α=2psinα,
64sin2α=16pcosα.
∴8sin3α=cos3α,即tanα=![]() .从而sinα=
.从而sinα=![]() ,cosα=
,cosα=![]() .
.
∴p=![]() ,得抛物线C的方程为y2=
,得抛物线C的方程为y2=![]() .
.
又直线l平分∠B′OB,得l的倾斜角为α+![]() +45°.
+45°.
∴k=tan(![]() +45°)=
+45°)=![]() .
.
∴直线l的方程为y=![]() x.
x.
方法归纳 (1)本题属于点关于直线的对称问题.利用对称图形的性质来解,它的技巧性较强,一时难于想到.
(2)本题是用待定系数法求直线的方程和抛物线方程.在已知曲线的类型求曲线方程时,这种方法是最常规方法,需要重点掌握.

练习册系列答案
相关题目
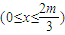 和椭圆弧
和椭圆弧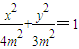

 和椭圆弧
和椭圆弧
