题目内容

数列{a_n}中，若a₁=-4，a_n+1=a_n+3，则|a₁|+|a₂|+…+|a₁₀|=

A.
23
B.
95
C.
100
D.
105

D
分析：先求数列的通项公式，再根据数列的通项公式弄清数列从第几项起符号发生改变，然后代入|a₁|+|a₂|+…+|a₁₀|求解即可．
解答：∵a₁=-4，a_n+1=a_n+3，∴a_n+1-a_n=3，
即数列{a_n}为-4为首项，3为公差的等差数列，
故a_n=-4+3（n-1）=3n-7，由3n-7＞0解得n＞ $\text{[math]}$ ，
∴数列{a_n}的前2项为负数，从第3项起为正数，
∴|a₁|+|a₂|+…+|a₁₀|
=-a₁-a₂+a₃+…+a₁₀
=（a₁+a₂+a₃+…+a₁₀）-2（a₁+a₂）
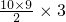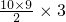=10×（-4）+ $\text{[math]}$ -2（-4-1）
=105
故选D
点评：本题考查数列的求和，解题的关键是弄清数列从第几项起符号发生改变，属于基础题．

练习册系列答案

中考数学合成演练30天系列答案

汇测期末竞优系列答案

素质提优123系列答案

随堂练123系列答案

随堂新卷系列答案

堂堂清课堂8分钟小测系列答案

特级教师小学毕业升学系统总复习系列答案

提分计划单元期末系列答案

经纶学典提优作业本系列答案

题粹系列答案

相关题目

数列{a_n}中，若

(n≥2，n∈N)，则a₂₀₁₃的值为（　　）

在数列{a_n}中，若a－a＝p(n≥2，n∈N^*，p为常数)，则{a_n}称为“等方差数列”，下列是对“等方差数列”的判断：

①若{a_n}是等方差数列，则{a}是等差数列；

②{(－1)ⁿ}是等方差数列；

③若{a_n}是等方差数列，则{a_kn}(k∈N^*，k为常数)也是等方差数列．

其中正确命题序号为________．(将所有正确的命题序号填在横线上)

在数列{a_n}中，若a－a＝p(n≥2，n∈N^*，p为常数)，则{a_n}称为“等方差数列”，下列是对“等方差数列”的判断：

①若{a_n}是等方差数列，则{a}是等差数列；

②{(－1)ⁿ}是等方差数列；

③若{a_n}是等方差数列，则{a_kn}(k∈N^*，k为常数)也是等方差数列．

其中正确命题序号为________．(将所有正确的命题序号填在横线上)

在数列{a_n}中，若a－a＝p，(n≥2，n∈N^*，p为常数)，则称{a_n}为“等方差数列”．下列是对“等方差数列”的判断：

①若{a_n}是等方差数列，则{a}是等差数列；

②{(－1)ⁿ}是等方差数列；

③若{a_n}是等方差数列，则{a_kn}(k∈N^*，k为常数)也是等方差数列；

④既是等方差数列、又是等差数列的数列{a_n}不存在；

其中正确命题序号为________．(将所有正确的命题序号填在横线上)．

在数列{a_n}中，若a－a＝p(n≥2，n∈N_＋，p为常数)，则称{a_n}为“等方差数列”.下列是对“等方差数列”的判断：

①若{a_n}是等方差数列，则{a}是等差数列；

②{(－1)ⁿ}是等方差数列；

③若{a_n}是等方差数列，则{a_kn}(k∈N_＋，k为常数)也是等方差数列；

④若{a_n}既是等方差数列，又是等差数列，则该数列为常数数列.

其中正确命题的序号为　　　　.(将所有正确命题的序号填在横线上).