题目内容
(本小题满分12分)设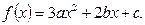 若
若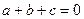
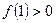 ,求证:
,求证:
(Ⅰ)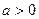 且
且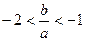 ;
;
(Ⅱ)方程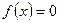 在
在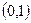 内有两个实根.
内有两个实根.
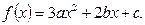 若
若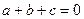
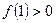 ,求证:
,求证:(Ⅰ)
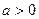 且
且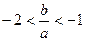 ;
;(Ⅱ)方程
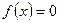 在
在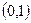 内有两个实根.
内有两个实根. (Ⅰ)因为 ,所以
,所以 .
.
由条件 ,消去
,消去 ,得
,得 ;
;
由条件 ,消去
,消去 ,得
,得 ,
, .
.
故 . ……6分
. ……6分
(Ⅱ)函数 的顶点坐标为
的顶点坐标为 ,
,
在 的两边乘以
的两边乘以 ,得
,得 .
.
又因为 而
而
又因为 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以方程 在区间
在区间 与
与 内分别各有一实根。
内分别各有一实根。
故方程 在
在 内有两个实根. ……12分
内有两个实根. ……12分
 ,所以
,所以 .
.由条件
 ,消去
,消去 ,得
,得 ;
;由条件
 ,消去
,消去 ,得
,得 ,
, .
.故
 . ……6分
. ……6分(Ⅱ)函数
 的顶点坐标为
的顶点坐标为 ,
,在
 的两边乘以
的两边乘以 ,得
,得 .
.又因为
 而
而
又因为
 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,所以方程
 在区间
在区间 与
与 内分别各有一实根。
内分别各有一实根。故方程
 在
在 内有两个实根. ……12分
内有两个实根. ……12分略

练习册系列答案
相关题目



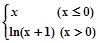 ,若f(2-x2)>f(x),则实数x的取值范围是( )
,若f(2-x2)>f(x),则实数x的取值范围是( )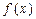 ,如果满足:对任意
,如果满足:对任意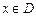 ,存在常数
,存在常数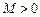 ,都有
,都有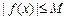 成立,则称
成立,则称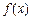 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数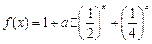 ;
;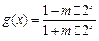 .
.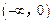 上的值域,并判断函数
上的值域,并判断函数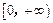 上是以3为上界的
上是以3为上界的 有界函数,求实数a的取值范围;
有界函数,求实数a的取值范围;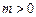 ,函
,函 数
数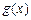 在
在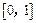 上的上界是
上的上界是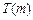 ,求
,求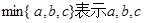 三个数中的最小值,设
三个数中的最小值,设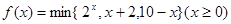 ,则
,则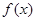 的最大值为 ( )
的最大值为 ( ) 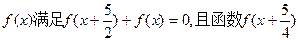 为奇函数.
为奇函数. 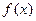 的最小正周期是
的最小正周期是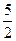 ;②函数
;②函数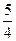 ,0)
,0)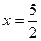 对称;④函数
对称;④函数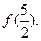

 ( )
( )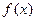 ,
,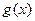 分别由下表给出
分别由下表给出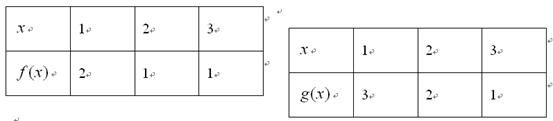
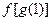 的值为 ;当
的值为 ;当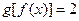 时,
时, .
.