Question

【题目】定义在上的函数满足，，则下列说法正确的是（ ）

A.在处取得极小值，极小值为

B.只有一个零点

C.若在上恒成立，则

D.

Answer 1

【答案】BCD

【解析】

对A，根据，，求，求出，根据极值定义进行判断；对B，根据单调性和零点定义，结合图象判断；对C，要保证在上恒成立，即，通过构造函数求其最值，进行判断；对D，根据单调性，和对数比较大小，进行判断.

对A，，且

可得：

可得：

故(为常数)

又

可得：

求得：

故：

整理可得：，

当，即

解得：，，此时单调递增

当，即

解得：，，

当，即

解得：，，此时单调递减

，取得极大值，，故A说法错误；

对B，，

，

，

画出草图：如图

根据图象可知：只有一个零点，故B说法正确；

对C，要保证在上恒成立

即：保证在上恒成立

，可得在上恒成立

故：只需

令

当时，

当时，

当时，

即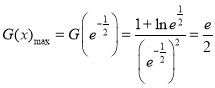

,故C说法正确；

对D，根据，单调递增，，单调递减，

，可得

又

由

根据

故：，故D说法正确.

综上所述，正确的说法是：BCD

故选：BCD.