题目内容
16．
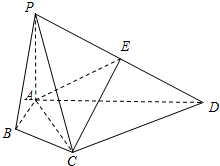在四棱锥P-ABCD中，PA⊥平面ABCD，E是PD的中点，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，AC=AP．（Ⅰ）求证：CE∥平面PAB；
（Ⅱ）求证：PC⊥AE．
分析 （Ⅰ）根据线面平行的判定定理即可证明CE∥平面PAB；
（Ⅱ）根据线面垂直的性质定理即可证明PC⊥AE．
解答 证明：（Ⅰ）取AD的中点M，连接CM，EM．则有 EM∥PA．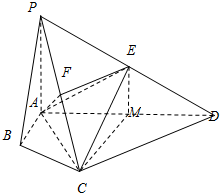
因为 PA?平面PAB，EM?平面PAB
所以EM∥平面PAB．…2分
由题意知∠BAC=∠CAD=∠ACM=60°，
所以 CM∥AB．
同理 CM∥平面PAB．…4分
又因为 CM?平面CME，EM?平面CME，CM∩EM=M
所以 平面CME∥平面PAB．
因为 CE?平面CME
所以 CE∥平面PAB． …6分
（Ⅱ）取PC的中点F，连接EF，AF，则EF∥CD．
因为AP=AC，所以 PC⊥AF．…7分
因为 PA⊥平面ABCD，CD?平面ABCD，所以 PA⊥CD
又 AC⊥CD
所以 CD⊥平面PAC…9分
因为PC?平面PAC所以 CD⊥PC
又 EF∥CD，所以 EF⊥PC
又因为PC⊥AF，AF∩EF=F
所以 PC⊥平面AEF…11分
因为AE?平面AEF
所以 PC⊥AE…12分．
点评 本题主要考查线面平行和线面垂直的判断，根据相应的判定定理是解决本题的关键．
练习册系列答案
相关题目
7．有一个7人学习合作小组，从中选取4人发言，要求其中组长和副组长至少有一人参加，若组长和副组长同时参加，则他们发言时顺序不能相邻，那么不同的发言顺序有（ ）
| A． | 720种 | B． | 600种 | C． | 360种 | D． | 300种 |
4．设{an}是等比数列，则对任何n∈N*，都有$\frac{1}{{{a_1}{a_2}}}•\frac{1}{{{a_2}{a_3}}}…\frac{1}{{{a_n}{a_{n+1}}}}$=（ ）
| A． | $\frac{1}{{{{（{a_1}•{a_n}）}^n}}}$ | B． | $\frac{1}{{{{（{a_1}•{a_{n+1}}）}^n}}}$ | C． | $\frac{1}{{{{（{a_1}•{a_n}）}^{n+1}}}}$ | D． | $\frac{1}{{{{（{a_1}•{a_{n+1}}）}^{n+1}}}}$ |
11．
某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务，为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n（单位：万次），整理后得到如图茎叶图，已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择．
（I）请说明A公司应选择哪个网站；
（Ⅱ）现将抽取的样本分布近似看作总体分布，A公司根据所选网站的日访问量n进行付费，其付费标准如下：
求A公司每月（按30天计）应付给选定网站的费用S．
某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务，为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n（单位：万次），整理后得到如图茎叶图，已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择．（I）请说明A公司应选择哪个网站；
（Ⅱ）现将抽取的样本分布近似看作总体分布，A公司根据所选网站的日访问量n进行付费，其付费标准如下：
| 选定网站的日访问量n（单位：万次） | A公司的付费标准（单位：元/日） |
| n＜25 | 500 |
| 25≤n≤35 | 700 |
| n＞35 | 1000 |
