题目内容
已知集合A={x|x2+a≤|a+1|x,a∈R}.(1)求A;
(2)若以a为首项,a为公比的等比数列的前n项和记为Sn,问是否存在a,使得对于任意的n∈N*,均有Sn∈A,若存在,求a的范围,若不存在,说明理由.
解:(1)由x2+a≤|a+1|x,a∈R得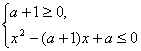 或
或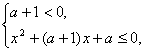
∴a>1时,1≤x≤a;-1≤a≤1时,a≤x≤1;a<-1时,-1≤x≤-a.
∴当a>1时,A={x|1≤x≤a};当-1≤a≤1时,A={x|a≤x≤1};当a<-1时,A={x|-1≤x≤-a}.
(2)①当a≥1时,A={x|a≤x≤1},而S2=a+a2>a,∴S2![]() A.
A.
②当0<a<1时,A={x|a≤x≤1},而Sn=a+a2+…+an是关于n的递增函数,
且![]() Sn=
Sn=![]() ,∴Sn∈[a,
,∴Sn∈[a,![]() ).
).
对于任意的n∈N*,Sn∈A只要a满足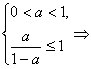 0<a≤
0<a≤![]() 为所求.
为所求.
③当a<-1时,A={x|-1≤x≤-a},S1=a![]() A,故不存在这样的a,使Sn∈A.
A,故不存在这样的a,使Sn∈A.
④当a=-1时,A={x|-1≤x≤1},S2n-1=-1,S2n=0适合,∴a=-1为所求.
⑤当-1<a<0时,A={x|a≤x≤1},
∵S2n+1=S2n-1+a2n+a2n+1=S2n-1+a2n+a2n+1=S2n-1+a2n(1+a)>S2n-1,
S2n+2=S2n+a2n+1+a2n+2=S2n+a2n+1+a2n+2=S2n+a2n+1(1+a)<S2n,
∴S2n+1>S2n-1,S2n+2<S2n,故S1<S3<…<S2n+1<S2n<S2n-2<…<S4<S2.
∴要使Sn∈A,只需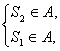 即
即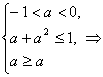 -1<a<0.
-1<a<0.
综上得-1≤a<0或0<a<![]() .
.

练习册系列答案
相关题目