题目内容
已知函数f(x)的图像如图所示，则f(x)的解析式可以是( )
A．f(x)＝x－ | B．f(x)＝ | C．f(x)＝ －1 | D．f(x)＝ |
D
解析
练习册系列答案
相关题目
定义域为
的偶函数
满足对
，有
，且当
时，
，若函数
至少有三个零点，则
的取值范围是( )
A． | B． | C． | D． |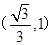
下列函数中，与函数y＝－3|x|的奇偶性相同，且在(－∞，0)上单调性也相同的是( )
A．y＝－ | B．y＝log2|x| |
| C．y＝1－x2 | D．y＝x3－1 |
已知函数f(x)=
若f(2-a2)>f(a),则实数a的取值范围是( )
| A．(-∞,-1)∪(2,+∞) |
| B．(-1,2) |
| C．(-2,1) |
| D．(-∞,-2)∪(1,+∞) |
函数f(x)＝x＋sin x(x∈R)( )
| A．是偶函数且为减函数 |
| B．是偶函数且为增函数 |
| C．是奇函数且为减函数 |
| D．是奇函数且为增函数 |
若函数y＝f(x)(x∈R)满足f(x＋1)＝f(x－1)，且x∈[－1，1]时，f(x)＝1－x2，函数g(x)＝
则函数h(x)＝f(x)－g(x)在区间[－5，5]内的零点的个数为( )
| A．6 | B．7 | C．8 | D．9， |
设奇函数f(x)在[－1，1]上是增函数，且f(－1)＝－1，若函数f(x)≤t2－2at＋1对所有的x∈[－1，1]都成立，则当a∈[－1，1]时t的取值范围是( )
| A．－2≤t≤2 | B．－ ≤t≤ |
| C．t≤－2或t＝0或t≥2 | D．t≤－或t＝0或t≥ |
已知函数f(x)＝ax＋x－b的零点x0∈(n，n＋1)(n∈Z)，其中常数a，b满足2a＝3,3b＝2.则n的值是 ( )．
| A．－2 | B．－1 | C．0 | D．1 |
设奇函数f(x)在[－1,1]上是增函数，且f(－1)＝－1，若函数f(x)≤t2－2at＋1对所有的x∈[－1,1]都成立，则当a∈[－1,1]时t的取值范围是( )．
| A．－2≤t≤2 | B．－ ≤t≤ |
| C．t≤－2或t＝0或t≥2 | D．t≤－或t＝0或t≥ |