题目内容
已知函数
，则使f（x+c）=f（x）恒成立的最小正数c=________．
2
分析：先由f（x+c）=f（x）确定c为函数f（x）的周期，明确题目要求的是函数的最小正周期，故先利用二倍角的余弦函数公式化简函数解析式，得到一个角的余弦函数，找出ω的值，代入周期公式T=
，求出函数的最小正周期，即为所求c的值．
解答：∵f（x+c）=f（x），∴函数f（x）的周期为c．
又=
cosπx+，
∵ω=π，∴T=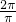
=2，
∴最小正数c要满足：c=2．
故答案为：2
点评：此题考查了三角函数的周期性及其求法，其中根据题意，明确要求的c即为函数的最小正周期是解本题的关键．
分析：先由f（x+c）=f（x）确定c为函数f（x）的周期，明确题目要求的是函数的最小正周期，故先利用二倍角的余弦函数公式化简函数解析式，得到一个角的余弦函数，找出ω的值，代入周期公式T=
，求出函数的最小正周期，即为所求c的值．解答：∵f（x+c）=f（x），∴函数f（x）的周期为c．
又
=cosπx+，∵ω=π，∴T=
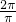=2，∴最小正数c要满足：c=2．
故答案为：2
点评：此题考查了三角函数的周期性及其求法，其中根据题意，明确要求的c即为函数的最小正周期是解本题的关键．
练习册系列答案
相关题目
，则使f(x)＜0的x的取值范围是________．
，则使f(x)＜0的x的取值范围是________．
为非零向量，函数
，则使f（x）的图象为关于y轴对称的抛物线的一个必要不充分条件是（ ）
，则使函数g（x）＝f（x）＋x－m有零点的实数m的取值范围是
B．
C．
D．