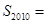题目内容
已知数列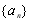 满足
满足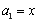 ,
, ,
, ,
,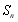 是数列
是数列 的前
的前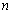 项和.
项和.
(1)若数列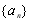 为等差数列.
为等差数列.
①求数列的通项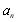 ;
;
②若数列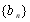 满足
满足 ,数列
,数列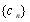 满足
满足 ,试比较数列
,试比较数列 前
前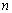 项和
项和 与
与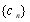 前
前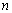 项和
项和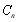 的大小;
的大小;
(2)若对任意 ,
,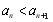 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
(1)①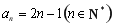
②当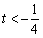 或
或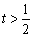 时,
时,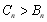 ;当
;当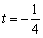 或
或 时,
时,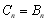 ;当
;当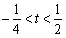 时,
时,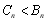
(2)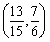
【解析】
试题分析:(1) 解等差数列问题,主要从待定系数对应关系出发.①从 与
与 关系出发,得出
关系出发,得出 ,利用
,利用 解出
解出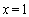 ,从而解出首项与公差,②
,从而解出首项与公差,② 实际是一个等比数列,分别求出数列
实际是一个等比数列,分别求出数列 前
前 项和
项和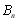 与
与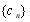 前
前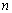 项和
项和 ,要使计算简便,需用
,要使计算简便,需用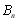 表示
表示 ,比较两者大小通常用作差法. 作差法的关键是因式分解,将差分解为因子,根据因子的符号讨论差的正负,从而确定大小,(2) 不等式恒成立问题,首先化简不等式. 需从
,比较两者大小通常用作差法. 作差法的关键是因式分解,将差分解为因子,根据因子的符号讨论差的正负,从而确定大小,(2) 不等式恒成立问题,首先化简不等式. 需从 与
与 关系出发,得出项的关系:
关系出发,得出项的关系: ,这是三项之间的关系,需继续化简成两项之间关系:
,这是三项之间的关系,需继续化简成两项之间关系: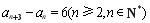 ,这样原数列分解为三个等差数列,则
,这样原数列分解为三个等差数列,则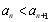 恒成立等价转化为
恒成立等价转化为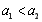 且
且 ,代入可解得
,代入可解得
试题解析:解:(1)因为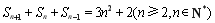 ,所以
,所以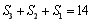 ,
,
即 ,又
,又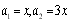 ,所以
,所以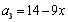 , 2分
, 2分
①又因为数列 成等差数列,所以
成等差数列,所以 ,即
,即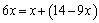 ,解得
,解得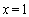 ,
,
所以 ; 4分
; 4分
②因为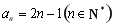 ,所以
,所以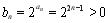 ,其前
,其前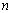 项和
项和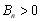 ,
,
又因为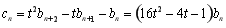 , 5分
, 5分
所以其前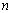 项和
项和 ,所以
,所以 , 7分
, 7分
当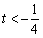 或
或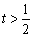 时,
时,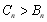 ;当
;当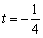 或
或 时,
时,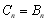 ;
;
当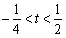 时,
时,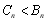 9分
9分
(2)由 知
知 ,
,
两式作差,得 , 10分
, 10分
所以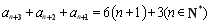 ,作差得
,作差得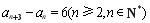 , 11分
, 11分
所以,当 时,
时, ;
;
当 时,
时, ;
;
当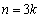 时,
时,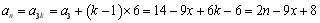 ;
;
当 时,
时, ; 14分
; 14分
因为对任意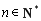 ,
,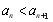 恒成立,所以
恒成立,所以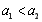 且
且 ,
,
所以 ,解得,
,解得, ,故实数
,故实数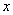 的取值范围为
的取值范围为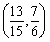 . 16分
. 16分
考点:等差数列通项,等比数列求和,不等式恒成立

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
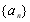

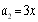
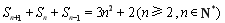
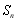
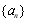
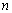
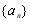
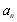
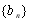
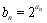
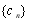
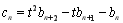
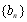
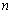
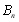
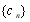
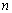
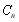
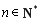
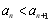
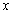
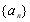
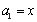
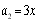
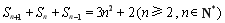
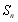
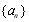
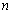
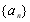
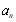
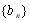
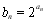
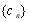
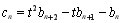
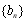
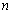
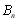
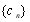
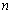
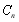
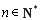
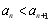
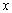
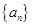 满足
满足 ,
,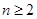 ,点
,点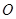 是平面上不在
是平面上不在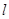 上的任意一点,
上的任意一点,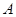 、
、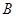 、
、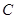 ,又知
,又知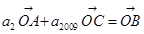 ,则
,则