题目内容
2．过点（-1，3）且横截距与纵截距相等的直线方程是3x+y=0，x+y-2=0．分析 当直线过原点（0，0）可设方程为y=kx，当直线不过原点，可设方程为$\frac{x}{a}$+$\frac{y}{a}$=1，分别代入点的坐标可求．
解答 解：当直线过原点（0，0）可设方程为y=kx，代入（-1，3）可得k=-3，
故直线方程为y=-3x，即3x+y=0；
当直线不过原点，可设方程为$\frac{x}{a}$+$\frac{y}{a}$=1，代入（-1，3）可得a=2，
故直线方程为$\frac{x}{2}$+$\frac{y}{2}$=1，即x+y-2=0，
故答案为：3x+y=0，x+y-2=0．
点评 本题考查直线的截距式方程，和化为一般式方程的能力，涉及分类讨论的思想，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
7．方程tanx+sinx-|tanx-sinx|+2lgx=0在[0，4π]上根的个数为（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
11．
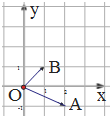如图，在复平面内，复数z1，z2对应的向量分别是$\overrightarrow{OA}$，$\overrightarrow{OB}$，设复数$z=\frac{z_1}{z_2}$，则z的共轭复数为（ ）
如图，在复平面内，复数z1，z2对应的向量分别是$\overrightarrow{OA}$，$\overrightarrow{OB}$，设复数$z=\frac{z_1}{z_2}$，则z的共轭复数为（ ）| A． | $\frac{1}{2}-\frac{3}{2}i$ | B． | $\frac{1}{2}+\frac{3}{2}i$ | C． | 1-3i | D． | 1+3i |