题目内容
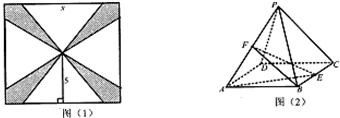
 用三个全等的等腰三角形拼接成一个正三棱锥形的漏斗(如图).已知三角形的一腰长为2.
用三个全等的等腰三角形拼接成一个正三棱锥形的漏斗(如图).已知三角形的一腰长为2.(Ⅰ)将漏斗容积V表示成关于三棱锥高h的函数关系式.
(Ⅱ)求漏斗容积的最大值,并求此时漏斗的高与等腰三角形的顶角大小.
分析:(Ⅰ)设出漏斗的上底面边长,结合腰长为2求出底边上的高,把底面边长用高表示,则可以求得漏斗容积V关于三棱锥高h的函数关系式.
(Ⅱ)求出V关于h的函数式的导函数,利用导函数判断出单调性,利用单调性求最值并求出漏斗的高与等腰三角形的顶角大小.
(Ⅱ)求出V关于h的函数式的导函数,利用导函数判断出单调性,利用单调性求最值并求出漏斗的高与等腰三角形的顶角大小.
解答:解:(Ⅰ)设等腰三角形的底边长为a,则三棱锥底面三角形边上的高为
a
∴(
×
a)2+h2=4,即h2+
a2=4
∴V=
×
×a2×h=
h(12-3h2)=
h-
h3(0<h<2);
(Ⅱ)∵V'=
-
h2,令V'=0,即h=
当0<h<
时,V'>0
当
<h<2时,V'<0
∴h=
时V取得极大值为
并且这个极大值是最大值
把h=
代入h2+
a2=4,得a=2
∴在△ASB中,∠ASB=
即漏斗容器的最大值为
,此时漏斗的高为
,等腰三角形的顶角为
.
| ||
| 2 |
∴(
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
∴V=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
| 3 |
| ||
| 4 |
(Ⅱ)∵V'=
| 3 |
3
| ||
| 4 |
| 2 |
| 3 |
| 3 |
当0<h<
| 2 |
| 3 |
| 3 |
当
| 2 |
| 3 |
| 3 |
∴h=
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
并且这个极大值是最大值
把h=
| 2 |
| 3 |
| 3 |
| 1 |
| 3 |
| 2 |
∴在△ASB中,∠ASB=
| π |
| 2 |
即漏斗容器的最大值为
| 4 |
| 3 |
| 2 |
| 3 |
| 3 |
| π |
| 2 |
点评:本题考查了锥体体积的表示方法,考查了利用导数求函数的最值,解答的关键是熟练掌握函数的单调性与导函数符号之间的关系,是中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
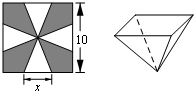 一个边长为10 cm的正方形铁片,把图中所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器.则这个容器侧面积S表示成x的函数为
一个边长为10 cm的正方形铁片,把图中所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器.则这个容器侧面积S表示成x的函数为