题目内容
已知
，若f'（-1）=8，则f（-1）=
- A.4
- B.5
- C.-2
- D.-3
A
分析：先求出函数的导数，再把x=-1代入 f′（x）的解析式得到f'（-1），再由f'（-1）=8，求得a的值，即可得到函数f（x）的解析式，从而求得f（-1）的值．
解答：已知，
∴f′（x）=3（2x+1）2×2+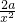
，
∵f'（-1）=8，
∴3×2+2a=8，故有a=1，
∴=
，
∴f（-1）=-1+2+3=4，
故选A．
点评：本题主要考查函数在某一点的导数的定义，求一个函数的导数的方法，属于基础题．
分析：先求出函数的导数，再把x=-1代入 f′（x）的解析式得到f'（-1），再由f'（-1）=8，求得a的值，即可得到函数f（x）的解析式，从而求得f（-1）的值．
解答：已知
，∴f′（x）=3（2x+1）2×2+
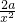，∵f'（-1）=8，
∴3×2+2a=8，故有a=1，
∴
=，∴f（-1）=-1+2+3=4，
故选A．
点评：本题主要考查函数在某一点的导数的定义，求一个函数的导数的方法，属于基础题．
练习册系列答案
相关题目
，若f'（-1）=8，则f（-1）=（ ）
，若f(x)=
?
+1，求：
，若f(x)=
?
+1，求：