题目内容
直线 相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn}.
相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn}.(1)当k=2时,求点P1,P2,P3的坐标并猜出点Pn的坐标;
(2)证明数列{xn-1}是等比数列,并求出数列{xn}的通项公式;
(3)比较
 的大小.
的大小.
【答案】分析:(1)根据直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,可得点P1,P2,P3的坐标,从而猜出点Pn的坐标;
(2)确定Qn,Pn+1的坐标,利用Pn+1在直线l1上,对其变形,即可证得结论;
(3)求出P的坐标,表示出 与
与 ,分类讨论,即可得到结论.
,分类讨论,即可得到结论.
解答:(1)解:由题意可 ,可猜得
,可猜得 .…(4分)
.…(4分)
(2)证明:设点Pn的坐标是(xn,yn),由已知条件得点Qn,Pn+1的坐标分别是: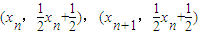 .
.
由Pn+1在直线l1上,得 .
.
所以 ,即
,即
所以数列{xn-1}是首项为x1-1,公比为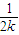 的等比数列.
的等比数列.
由题设知 ,
,
从而 ,∴
,∴ .…(9分)
.…(9分)
(3)解:由 得点P的坐标为(1,1).
得点P的坐标为(1,1).
所以 ,
, .
.
(i)当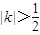 ,即
,即 或
或 时,
时, >1+9=10,
>1+9=10,
而此时 ,∴
,∴ ,
,
∴ .
.
(ii)当 ,∴
,∴ 时,
时, <1+9=10.
<1+9=10.
而此时 ,∴
,∴ ,
,
∴ .…(14分)
.…(14分)
点评:本题考查等比数列的证明,考查大小比较,考查学生分析解决问题的能力,考查分类讨论的数学思想,属于中档题.
(2)确定Qn,Pn+1的坐标,利用Pn+1在直线l1上,对其变形,即可证得结论;
(3)求出P的坐标,表示出
 与
与 ,分类讨论,即可得到结论.
,分类讨论,即可得到结论.解答:(1)解:由题意可
 ,可猜得
,可猜得 .…(4分)
.…(4分)(2)证明:设点Pn的坐标是(xn,yn),由已知条件得点Qn,Pn+1的坐标分别是:
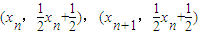 .
.由Pn+1在直线l1上,得
 .
.所以
 ,即
,即
所以数列{xn-1}是首项为x1-1,公比为
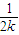 的等比数列.
的等比数列.由题设知
 ,
,从而
 ,∴
,∴ .…(9分)
.…(9分)(3)解:由
 得点P的坐标为(1,1).
得点P的坐标为(1,1).所以
 ,
, .
.(i)当
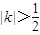 ,即
,即 或
或 时,
时, >1+9=10,
>1+9=10,而此时
 ,∴
,∴ ,
,∴
 .
.(ii)当
 ,∴
,∴ 时,
时, <1+9=10.
<1+9=10.而此时
 ,∴
,∴ ,
,∴
 .…(14分)
.…(14分)点评:本题考查等比数列的证明,考查大小比较,考查学生分析解决问题的能力,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn}.
相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn}. ;
;