设f′的导函数.y=f′(x)的图象如图所示.则y=f(x)的图象最有可能的是题目和参考答案——青夏教育精英家教网—

题目内容

设f′（x）是函数f（x）的导函数，y=f′（x）的图象如图所示，则y=f（x）的图象最有可能的是（）

解析试题分析：由f′（x）的图象可得，在（-∞，0）上，f′（x）＞0，f（x）是增函数．
在（0，2）上，f′（x）＜0，f（x）是减函数．
在（2，+∞）上，f′（x）＞0，f（x）是增函数．故选C．
考点：导数研究函数的单调性

练习册系列答案

湘岳中考系列答案

相关题目

（本小题满分12分）
已知命题 ,命题,
若命题是真命题,求实数a的取值范围.

(12分)设命题p：(4x－3)²≤1；命题q：x²－(2a＋1)x＋a(a＋1)≤0，若的必要不充分条件，求实数a的取值范围.

设f(x)是定义在Ｒ上的奇函数，当时，则=（）.

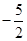已知函数的图象如右图，下列结论成立的是（）

A．	B．
C．	D．

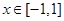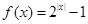已知函数是周期为2的周期函数，且当时，，则函数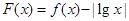的零点个数是（）

下列函数中，既是偶函数，又在区间(1，2)内是增函数的为( ).

A．y＝cos2x，x∈R	B．y＝log₂\|x\|，x∈R且x≠0)
C．y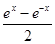＝，x∈R	D．y＝x³＋1，x∈R

已知实数,命题有两个不同的的实数根；
命题。若为真，为假，求的取值范围。

已知函数y＝f(x)的周期为2，当x∈[－1,1]时f(x)＝x²，那么函数y＝f(x)的图象与函数y＝|lg x|的图象的交点共有(　　)

试题分类