题目内容
函数f(x)=lg(1+x2),g(x)=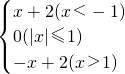 ,h(x)=tan2x中,________是奇函数,________是偶函数.
,h(x)=tan2x中,________是奇函数,________是偶函数.
h(x) g(x),f(x)
分析:用函数奇偶性定义判断.f(x),h(x)判断时,先看定义域,再研究关系;g(x)判断时,要注意从三种情况判断,即从1°当-1≤x≤1时;2°当x<-1时;3°当x>1时判断.
解答:函数f(x)=lg(1+x2),∵f(-x)=lg[1+(-x)2]=lg(1+x2)=f(x),∴f(x)为偶函数.
函数g(x)=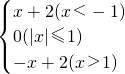 ,∵1°当-1≤x≤1时,-1≤-x≤1,∴g(-x)=0.又g(x)=0,∴g(-x)=g(x).
,∵1°当-1≤x≤1时,-1≤-x≤1,∴g(-x)=0.又g(x)=0,∴g(-x)=g(x).
2°当x<-1时,-x>1,∴g(-x)=-(-x)+2=x+2.又∵g(x)=x+2,∴g(-x)=g(x).
3°当x>1时,-x<-1,∴g(-x)=(-x)+2=-x+2.又∵g(x)=-x+2,∴g(-x)=g(x).
综上,对任意x∈R都有g(-x)=g(x),∴g(x)为偶函数.
函数h(x)=tan2x,∵h(-x)=tan(-2x)=-tan2x=-h(x),∴h(x)为奇函数.
故答案为:h(x);g(x),f(x)
点评:本题以函数为载体,考查函数奇偶性的判断,应先判断函数的定义域关于原点对称,再合理运用定义,要注意分段函数的判断,需分段研究.
分析:用函数奇偶性定义判断.f(x),h(x)判断时,先看定义域,再研究关系;g(x)判断时,要注意从三种情况判断,即从1°当-1≤x≤1时;2°当x<-1时;3°当x>1时判断.
解答:函数f(x)=lg(1+x2),∵f(-x)=lg[1+(-x)2]=lg(1+x2)=f(x),∴f(x)为偶函数.
函数g(x)=
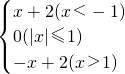 ,∵1°当-1≤x≤1时,-1≤-x≤1,∴g(-x)=0.又g(x)=0,∴g(-x)=g(x).
,∵1°当-1≤x≤1时,-1≤-x≤1,∴g(-x)=0.又g(x)=0,∴g(-x)=g(x).2°当x<-1时,-x>1,∴g(-x)=-(-x)+2=x+2.又∵g(x)=x+2,∴g(-x)=g(x).
3°当x>1时,-x<-1,∴g(-x)=(-x)+2=-x+2.又∵g(x)=-x+2,∴g(-x)=g(x).
综上,对任意x∈R都有g(-x)=g(x),∴g(x)为偶函数.
函数h(x)=tan2x,∵h(-x)=tan(-2x)=-tan2x=-h(x),∴h(x)为奇函数.
故答案为:h(x);g(x),f(x)
点评:本题以函数为载体,考查函数奇偶性的判断,应先判断函数的定义域关于原点对称,再合理运用定义,要注意分段函数的判断,需分段研究.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目