题目内容
已知函数f(x)=2+ ,数列{an}满足a1=1,
,数列{an}满足a1=1, =f(an)(n∈N*).
=f(an)(n∈N*).
(1)证明:数列{ }是等差数列;
}是等差数列;
(2)记Sn=a1a2+a2a3+…anan+1,求Sn.
(1)证明:因为f(x)=2+ ,
,
由 =f(an)得,
=f(an)得, ,
,
即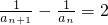 (n∈N*),
(n∈N*),
所以,数列{ }是公差为2的等差数列;
}是公差为2的等差数列;
(2)解:由数列{ }是公差为2的等差数列,
}是公差为2的等差数列,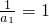 .
.
所以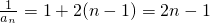 .
.
则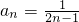 .
.
 =
=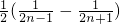
所以,Sn=a1a2+a2a3+…+anan+1
=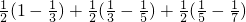 +
+
=
=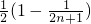
= .
.
分析:(1)由f(x)=2+ ,
, =f(an)联立可得递推式
=f(an)联立可得递推式 ,移向后即可得到结论;
,移向后即可得到结论;
(2)由数列{ }是等差数列求出an,把an代入Sn=a1a2+a2a3+…anan+1,利用裂项相消可求前n项和.
}是等差数列求出an,把an代入Sn=a1a2+a2a3+…anan+1,利用裂项相消可求前n项和.
点评:本题考查了数列的函数特性,考查了等差数列的通项公式,训练了裂项相消求数列的前n项和,此题是中档题.
 ,
,由
 =f(an)得,
=f(an)得, ,
,即
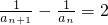 (n∈N*),
(n∈N*),所以,数列{
 }是公差为2的等差数列;
}是公差为2的等差数列;(2)解:由数列{
 }是公差为2的等差数列,
}是公差为2的等差数列,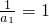 .
.所以
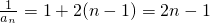 .
.则
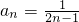 .
. =
=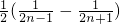
所以,Sn=a1a2+a2a3+…+anan+1
=
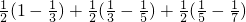 +
+
=

=
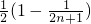
=
 .
.分析:(1)由f(x)=2+
 ,
, =f(an)联立可得递推式
=f(an)联立可得递推式 ,移向后即可得到结论;
,移向后即可得到结论;(2)由数列{
 }是等差数列求出an,把an代入Sn=a1a2+a2a3+…anan+1,利用裂项相消可求前n项和.
}是等差数列求出an,把an代入Sn=a1a2+a2a3+…anan+1,利用裂项相消可求前n项和.点评:本题考查了数列的函数特性,考查了等差数列的通项公式,训练了裂项相消求数列的前n项和,此题是中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目