题目内容
定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是![]() ,且当x∈
,且当x∈![]() 时,f(x)=sinx.
时,f(x)=sinx.
(1)求当x∈[-![]() ,0]时,f(x)的解析式;
,0]时,f(x)的解析式;
(2)画出函数f(x)在[-![]() ,
,![]() ]上的函数简图;
]上的函数简图;
(3)求当f(x)≥![]() 时,x的取值范围.
时,x的取值范围.
(1)f(x)=-sinx(2)见解析(3)当x∈![]() ,k∈Z时,f(x)≥
,k∈Z时,f(x)≥![]()
解析:
(1)∵f(x)是偶函数,∴f(-x)=f(x).
而当x∈![]() 时,f(x)=sinx.∴当x∈
时,f(x)=sinx.∴当x∈![]() 时,
时,
f(x)=f(-x)=sin(-x)=-sinx.
又当x∈![]() 时,x+
时,x+![]() ∈
∈![]() ,
,
∵f(x)的周期为![]() ,∴f(x)=f(
,∴f(x)=f(![]() +x)=sin(
+x)=sin(![]() +x)=-sinx.
+x)=-sinx.
∴当x∈[-![]() ,0]时,f(x)=-sinx.
,0]时,f(x)=-sinx.
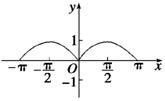 (2)如图:
(2)如图:
(3)由于f(x)的最小正周期为![]() ,
,
因此先在[-![]() ,0]上来研究f(x)≥
,0]上来研究f(x)≥![]() ,
,
即-sinx≥![]() ,∴sinx≤-
,∴sinx≤-![]() ,∴-
,∴-![]() ≤x≤-
≤x≤-![]() .
.
由周期性知,
当x∈![]() ,k∈Z时,f(x)≥
,k∈Z时,f(x)≥![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目