题目内容
已知数列{an}满足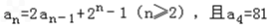 .
.
(I)求数列的前三项a1,a2,a3;
(II)求证:数列 为等差数列;
为等差数列;
(III)求数列{an}的前n项和Sn.
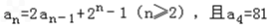 .
.(I)求数列的前三项a1,a2,a3;
(II)求证:数列
 为等差数列;
为等差数列;(III)求数列{an}的前n项和Sn.
解:(I)由 an=2an﹣1+2n﹣1(n∈N+,且n≥2)得 a4=2a3+24﹣1=81,得a3=33,
同理,可得 a2=13,a1=5.
(II)∵an=2an﹣1+2n﹣1,
∴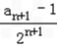 ﹣
﹣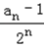 =
= 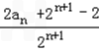 ﹣
﹣ =1,
=1,
故数列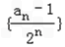 是以2为首项,以1为公差的等差数列.
是以2为首项,以1为公差的等差数列.
(III)由(II)可得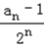 =2+(n﹣1)×1,
=2+(n﹣1)×1,
∴an=(n+1)2n+1.
∴Sn=a1+a2+…+an=2×2+3×22+4×23+…+(n+1)×2n+n,
记Tn=2×2+3×22+4×23+…+(n+1)×2n,
则有2Tn=2×22+3×23+…+n×2n +(n+1)2n+1.
两式相减,
可得﹣Tn=2×2+22+23+…+2n﹣(n+1)2n+1=4+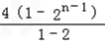 ﹣(n+1)2n+1=﹣n·2n+1,
﹣(n+1)2n+1=﹣n·2n+1,
解得 Tn=n×2n+1,故 Sn=Tn+n=n×2n+1+n=n?(2n+1+1 ).
同理,可得 a2=13,a1=5.
(II)∵an=2an﹣1+2n﹣1,
∴
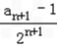 ﹣
﹣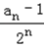 =
= 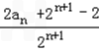 ﹣
﹣ =1,
=1,故数列
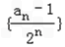 是以2为首项,以1为公差的等差数列.
是以2为首项,以1为公差的等差数列.(III)由(II)可得
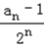 =2+(n﹣1)×1,
=2+(n﹣1)×1, ∴an=(n+1)2n+1.
∴Sn=a1+a2+…+an=2×2+3×22+4×23+…+(n+1)×2n+n,
记Tn=2×2+3×22+4×23+…+(n+1)×2n,
则有2Tn=2×22+3×23+…+n×2n +(n+1)2n+1.
两式相减,
可得﹣Tn=2×2+22+23+…+2n﹣(n+1)2n+1=4+
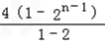 ﹣(n+1)2n+1=﹣n·2n+1,
﹣(n+1)2n+1=﹣n·2n+1,解得 Tn=n×2n+1,故 Sn=Tn+n=n×2n+1+n=n?(2n+1+1 ).

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目