题目内容
已知正三棱柱ABC—A1B1C1中,D是AB的中点,DC=?DA1=a?,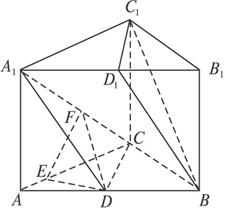
(1)求异面直线BC1与A1D所成的角;
(2)求二面角D-A1C-A的大小;
(3)求点C1到平面A1DC的距离.
解:(1)∵ABC—A1B1C1是正三棱柱,且D是AB的中点,

∴AB=BC=AC=![]() a.又DA1=a,
a.又DA1=a,
∴CC1=AA1=![]() =
=![]() a,且BC1=
a,且BC1=![]() =
=![]() a.
a.
取A1B1的中点D1,连结BD1,则BD1∥A1D,∴∠D1BC1是异面直线BC1与A1D所成的角.∵D1是A1B1的中点,∴△BD1C1是直角三角形.在Rt△BD1C1中,C1D1=BD1=a,BC1=![]() a,
a,
∴∠D1BC1=45°,即异面直线BC1与A1D所成的角为45°
(2)过点D作DE⊥AC于E,过E作EF⊥A1C于F,连结DF.
∵ABC—A1B1C1是正三棱柱,且DE⊥AC,∴DE⊥面ACA1.又EF⊥A1C,由三垂线定理,得DF⊥A1C,∠EFD是二面角DA1CA的平面角.在△EFD中,DE=![]() a,DF=
a,DF=![]() a,∠DEF=90°,
a,∠DEF=90°,
∴∠DEF=45°,即二面角D-A1C-A的大小为45°.
(3)∵AC1的中点M在平面AD1C上,∴点C1到平面的距离即为点A到平面AD1C的距离.
过A作AH⊥A1D,垂足为H,∵平面AD1C⊥平面AA1B1B,∴AH即为所求.
AH=![]() a,故点C1到平面A1DC的距离是
a,故点C1到平面A1DC的距离是![]() a.
a.

练习册系列答案
相关题目
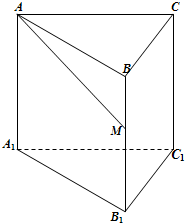 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ. 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.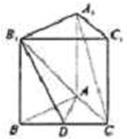 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.