题目内容
设函数y=f(x)= +a(
+a( +
+ ),a∈R
),a∈R
(Ⅰ)设t= +
+ ,把y表示成t的函数,并求出t的取值范围;
,把y表示成t的函数,并求出t的取值范围;
(Ⅱ)设f(x)的最小值为g(a),求g(a)的解析式,并求g(a)的值域.
解:(I)由t= +
+ 两边同时平方可得,
两边同时平方可得,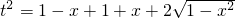 =
=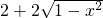
∴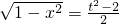
∵f(x)= +a(
+a( +
+ )
)
=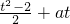 =
=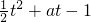
∵0≤1-x2≤1
∴2≤t2≤4且t>0
∴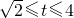
∴y=f(t)=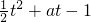 ,
,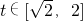
(II)∵y=f(t)=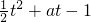 ,
,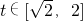
=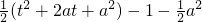 =
=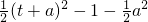
①当-a≥2即a≤-2时,函数f(t)在[ ]单调递减,g(a)=f(2)=2a+1≤-3
]单调递减,g(a)=f(2)=2a+1≤-3
②当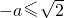 即a
即a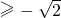 时,函数f(t)在[
时,函数f(t)在[ ]单调递增,g(a)=f(
]单调递增,g(a)=f( )=
)= ≥-2
≥-2
③当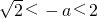 即-2<a<-
即-2<a<- 时,g(a)=f(-a)=
时,g(a)=f(-a)=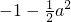 ∈(-3,-2)
∈(-3,-2)
根据分段函数的性质可知,分段函数的值域是各段函数值域的并集
∴g(a)的值域为R
分析:(I)对t= +
+ 两边同时平方可得t与x的关系,代入已知函数中即可求解f(t),
两边同时平方可得t与x的关系,代入已知函数中即可求解f(t),
(2)由(I)可得f(t)与t的关系及t的范围,然后结合二次函数的性质可求函数的最小值g(a)
点评:本题主要考查了换元法在求解函数值域中的应用,二次函数在闭区间上最值的求解,体现了分类讨论思想的应用.
 +
+ 两边同时平方可得,
两边同时平方可得,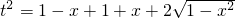 =
=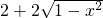
∴
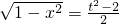
∵f(x)=
 +a(
+a( +
+ )
)=
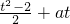 =
=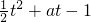
∵0≤1-x2≤1
∴2≤t2≤4且t>0
∴
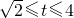
∴y=f(t)=
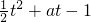 ,
,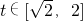
(II)∵y=f(t)=
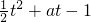 ,
,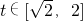
=
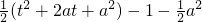 =
=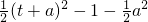
①当-a≥2即a≤-2时,函数f(t)在[
 ]单调递减,g(a)=f(2)=2a+1≤-3
]单调递减,g(a)=f(2)=2a+1≤-3②当
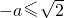 即a
即a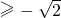 时,函数f(t)在[
时,函数f(t)在[ ]单调递增,g(a)=f(
]单调递增,g(a)=f( )=
)= ≥-2
≥-2③当
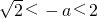 即-2<a<-
即-2<a<- 时,g(a)=f(-a)=
时,g(a)=f(-a)=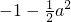 ∈(-3,-2)
∈(-3,-2)根据分段函数的性质可知,分段函数的值域是各段函数值域的并集
∴g(a)的值域为R
分析:(I)对t=
 +
+ 两边同时平方可得t与x的关系,代入已知函数中即可求解f(t),
两边同时平方可得t与x的关系,代入已知函数中即可求解f(t),(2)由(I)可得f(t)与t的关系及t的范围,然后结合二次函数的性质可求函数的最小值g(a)
点评:本题主要考查了换元法在求解函数值域中的应用,二次函数在闭区间上最值的求解,体现了分类讨论思想的应用.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目