题目内容
给出下列四个命题:
(1)函数y=sin(kπ+x),(k∈Z)是奇函数;
(2)函数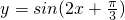 的图象由y=sin2x的图象向左平移
的图象由y=sin2x的图象向左平移 个单位得到;
个单位得到;
(3)函数 的对称轴是
的对称轴是 ;
;
(4)函数y=(sinx+cosx)2+cos2x的最大值为3.
其中正确命题的序号是________(把你认为正确的命题序号都填上).
解:(1)∵函数y=sin(kπ+x)=(-1)ksinx(k∈Z),∴f(-x)=(-1)ksin(-x)=-(-1)ksinx=-f(x),故是奇函数,正确;
(2)由y=sin2x的图象向左平移 个单位得到y=
个单位得到y= =
= ≠
≠ ,因此(2)不正确;
,因此(2)不正确;
(3)由 ,解得
,解得 ,(k∈Z),故函数
,(k∈Z),故函数 的对称轴是
的对称轴是 ,因此(3)正确;
,因此(3)正确;
(4)∵函数y=(sinx+cosx)2+cos2x=1+sin2x+cos2x= ,当
,当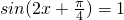 时,函数y=(sinx+cosx)2+cos2x的最大值为
时,函数y=(sinx+cosx)2+cos2x的最大值为 ,因此(4)不正确.
,因此(4)不正确.
综上可知:正确的命题为(1)(3).
故答案为(1)(3).
分析:(1)利用奇函数的定义即可判断;
(2)利用平移变换“左加右减”即可判断出;
(3)经过函数 的图象的最高点或最低点且与y轴平行的直线是其对称轴,先求出即可判断;
的图象的最高点或最低点且与y轴平行的直线是其对称轴,先求出即可判断;
(4)先化简,进而利用三角函数的最值即可判断.
点评:熟练掌握三角函数的图象与性质及其变换是解题的关键.
(2)由y=sin2x的图象向左平移
 个单位得到y=
个单位得到y= =
= ≠
≠ ,因此(2)不正确;
,因此(2)不正确;(3)由
 ,解得
,解得 ,(k∈Z),故函数
,(k∈Z),故函数 的对称轴是
的对称轴是 ,因此(3)正确;
,因此(3)正确;(4)∵函数y=(sinx+cosx)2+cos2x=1+sin2x+cos2x=
 ,当
,当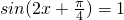 时,函数y=(sinx+cosx)2+cos2x的最大值为
时,函数y=(sinx+cosx)2+cos2x的最大值为 ,因此(4)不正确.
,因此(4)不正确.综上可知:正确的命题为(1)(3).
故答案为(1)(3).
分析:(1)利用奇函数的定义即可判断;
(2)利用平移变换“左加右减”即可判断出;
(3)经过函数
 的图象的最高点或最低点且与y轴平行的直线是其对称轴,先求出即可判断;
的图象的最高点或最低点且与y轴平行的直线是其对称轴,先求出即可判断;(4)先化简,进而利用三角函数的最值即可判断.
点评:熟练掌握三角函数的图象与性质及其变换是解题的关键.

练习册系列答案
相关题目