题目内容
函数f(x)=log2(1+x),g(x)=log2(1﹣x),则f(x)﹣g(x)是( )
|
| A. | 奇函数 | B. | 偶函数 |
|
| C. | 既不是奇函数又不是偶函数 | D. | 既是奇函数又是偶函数 |
A【解析】∵f(x)=log2(1+x),g(x)=log2(1﹣x),
∴f(x)﹣g(x)的定义域为(﹣1,1)
记F(x)=f(x)﹣g(x)=log2 ,
,
则F(﹣x)=log2 =log2(
=log2( )﹣1=﹣log2
)﹣1=﹣log2 =﹣F(x)
=﹣F(x)
故f(x)﹣g(x)是奇函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
根据空气质量指数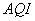 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
|
|
|
|
|
|
|
|
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
某市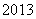 年
年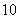 月
月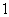 日—
日—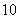 月
月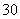 日,对空气质量指数
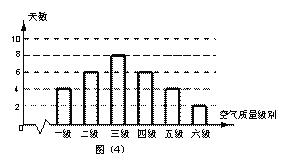
日,对空气质量指数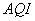 进行监测,获得数据后得到如图(4)的条形图
进行监测,获得数据后得到如图(4)的条形图
(1)估计该城市本月(按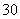 天计)空气质量类别为中度污染的概率;
天计)空气质量类别为中度污染的概率;
(2)在空气质量类别颜色为紫色和褐红色的数据中任取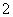 个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.
个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.
 ,若
,若 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围
的取值范围 或
或 (B)
(B) (C)
(C) (D)
(D) 或
或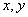 满足线性约束条件
满足线性约束条件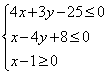 ,则
,则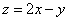 的最大值为________.
的最大值为________.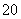 的样本.已知乙层中每个个体被抽到的概率都为
的样本.已知乙层中每个个体被抽到的概率都为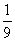 ,则总体中的个体数为 .
,则总体中的个体数为 .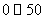

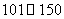
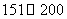
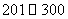
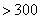
 的二项展开式中x4项的系数为20,则a= .
的二项展开式中x4项的系数为20,则a= . 的两个根,且A+B=120°,求△ABC的面积及AB的长.
的两个根,且A+B=120°,求△ABC的面积及AB的长. 的离心率为
的离心率为 ,则m等于 _________ .
,则m等于 _________ .