题目内容
设F1、F2分别是椭圆 (a>b>0)的左、右焦点,与直线y=b相切的⊙F2交椭圆于点E,且E是直线EF1与⊙F2的切点,则椭圆的离心率为________.
(a>b>0)的左、右焦点,与直线y=b相切的⊙F2交椭圆于点E,且E是直线EF1与⊙F2的切点,则椭圆的离心率为________.

分析:作出图形,根据椭圆的定义,可得到EF1+EF2=2a,依题意
 +
+ =
= =4c2,再由⊙F2与直线y=b相切,可得EF2=b,
=4c2,再由⊙F2与直线y=b相切,可得EF2=b,从而有(2a-b)2+b2=4c2,整理即可求得椭圆的离心率.
解答:
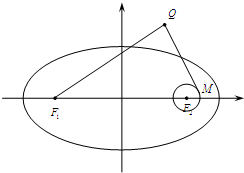
 解:依题意,作图如右:
解:依题意,作图如右:∵EF1⊥EF2,⊙F2交椭圆于点E,
∴EF1+EF2=2a,
 +
+ =
= =(2c)2=4c2.①
=(2c)2=4c2.①又⊙F2与直线y=b相切,
∴EF2=b,②
∴EF1=2a-b,③
将②③代入①得:(2a-b)2+b2=4c2,
∴4a2+2b2-4ab=4c2,
∴2(a2-c2)=b(2a-b),即2b2=b(2a-b),
∵b≠0,
∴3b=2a,
∴4a2=9b2=9(a2-c2),
∴5a2=9c2,即e2=
 =
= ,
,∴e=
 =
= .
.点评:本题考查椭圆的简单性质,考查椭圆的定义,考查直线与圆相切,考查方程思想与数形结合思想的运用,属于难题.

练习册系列答案
相关题目
设F1、F2分别是椭圆
+
=1(a>b>0)的左、右焦点,P是其右准线上纵坐标为
c(c为半焦距)的点,且|F1F2|=|F2P|,则椭圆的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 设F1、F2分别是椭圆
设F1、F2分别是椭圆