题目内容
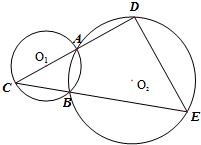 如图,A、B是两圆O1、O2的交点,AC是小圆O1的直径,D和E分别是CA和CB的延长线与大圆O2的交点,已知AC=2,BE=5,且BC=AD.
如图,A、B是两圆O1、O2的交点,AC是小圆O1的直径,D和E分别是CA和CB的延长线与大圆O2的交点,已知AC=2,BE=5,且BC=AD.(Ⅰ)求DE的长;
(Ⅱ)求圆O2的面积.
分析:(1)首先根据题中圆的切线条件再依据切割线定理求得一个线段的等式,再根据线段的关系可求得DE的长度即可.
(2)由AE为圆O2的直径得,直角三角形ADE,再结合勾股定理即可求得圆的直径,从而求出圆的面积.
(2)由AE为圆O2的直径得,直角三角形ADE,再结合勾股定理即可求得圆的直径,从而求出圆的面积.
解答:解:(Ⅰ)连接AB,设CB=AD=x,
由切割线定理得,CA•CD=CB•CE,即2(2+x)=x(x+5),(2分)
解得x=1或x=-4(舍去),即CD=3,CE=6,
∵CA是直径,
∴∠CBA=90°,即∠D=90°,(4分)
∴CD2+DE2=CE2,∴DE=3
.(6分)
(Ⅱ)连接AE,
∵∠D=90°,AE为圆O2的直径,(8分)
∵AD2+DE2=AE2,
∴AE2=28,
∴圆O2的面积为7π.(10分)
由切割线定理得,CA•CD=CB•CE,即2(2+x)=x(x+5),(2分)
解得x=1或x=-4(舍去),即CD=3,CE=6,
∵CA是直径,
∴∠CBA=90°,即∠D=90°,(4分)
∴CD2+DE2=CE2,∴DE=3
| 3 |
(Ⅱ)连接AE,
∵∠D=90°,AE为圆O2的直径,(8分)
∵AD2+DE2=AE2,
∴AE2=28,
∴圆O2的面积为7π.(10分)
点评:本题考查与圆有关的比例线段、平面几何的切割线定理,属容易题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
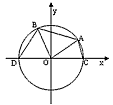
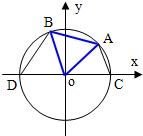 如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形.
如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形. 如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形.
如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形.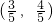 ,求cos∠BOC的值;
,求cos∠BOC的值; ),四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值.
),四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值.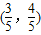 ,求cos∠BOC的值;
,求cos∠BOC的值; ),四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值.
),四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值.
 ,求cos∠BOC的值;
,求cos∠BOC的值; ),四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值.
),四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值.
 ,求cos∠BOC的值;
,求cos∠BOC的值;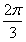 ),四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值。
),四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值。