题目内容
已知椭圆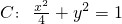 ,左右焦点分别为F1,F2,
,左右焦点分别为F1,F2,
(1)若C上一点P满足∠F1PF2=90°,求△F1PF2的面积;
(2)直线l交C于点A,B,线段AB的中点为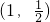 ,求直线l的方程.
,求直线l的方程.
解:(1)由第一定义,|PF1|+|PF2|=2a=4,即
由勾股定理, ,
,
∴|PF1||PF2|=2, .
.
(2)设A(x1,y1),B(x2,y2),满足 ,
, ,
,
两式作差 ,
,
将x1+x2=2,y1+y2=1代入,得 ,可得
,可得 ,
,
∴直线方程为: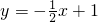 .
.
分析:(1)利用椭圆的定义和勾股定理及三角形的面积公式即可得出;
(2)利用“点差法”求出直线的斜率,进而利用点斜式即可求出直线的方程.
点评:熟练掌握椭圆的定义和勾股定理及三角形的面积公式、“点差法”求直线的斜率是解题的关键.

由勾股定理,
 ,
,∴|PF1||PF2|=2,
 .
.(2)设A(x1,y1),B(x2,y2),满足
 ,
, ,
,两式作差
 ,
,将x1+x2=2,y1+y2=1代入,得
 ,可得
,可得 ,
,∴直线方程为:
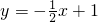 .
.分析:(1)利用椭圆的定义和勾股定理及三角形的面积公式即可得出;
(2)利用“点差法”求出直线的斜率,进而利用点斜式即可求出直线的方程.
点评:熟练掌握椭圆的定义和勾股定理及三角形的面积公式、“点差法”求直线的斜率是解题的关键.

练习册系列答案
相关题目


 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点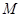 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的周长为6.
的周长为6.
 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值, 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.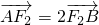 ,求k的值.
,求k的值.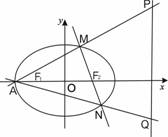 已知椭圆
已知椭圆 已知椭圆
已知椭圆 已知椭圆
已知椭圆