题目内容
已知椭圆E：
+
=1的左、右焦点分别为F1、F2，点P为椭圆上一点，若以（1，0）为圆心的圆C与直线PF1，PF2均相切，则点P的横坐标为（ ）
| x2 |
| 8 |
| y2 |
| 4 |
分析：设出P的坐标，利用圆心到直线的距离相等，求出关系式，利用P点在椭圆上得到关系式，解方程组可求P的坐标．
解答：解：设P（m，n），因为P在椭圆上所以
+
=1…①，
PF1的方程为y=
(x+2)，即nx-（m+2）y+2n=0，
PF2，的方程为y=
(x-2)，即nx-（m-2）y-2n=0，
因为以（1，0）为圆心的圆C与直线PF1，PF2均相切，
所以
=
，即3n2+3（m-2）2=n2+（m+2）2…②
解①②得，m=2，n=±
，
所求点P的横坐标为2．
故选B．
| m2 |
| 8 |
| n2 |
| 4 |
PF1的方程为y=
| n |
| m+2 |
PF2，的方程为y=
| n |
| m-2 |
因为以（1，0）为圆心的圆C与直线PF1，PF2均相切，
所以
| |n-2n| | ||
|
| |n+2n| | ||
|
解①②得，m=2，n=±
| 2 |
所求点P的横坐标为2．
故选B．
点评：本题考查椭圆的基本性质，点到直线的距离公式的应用，直线与圆的位置关系，直线与圆锥曲线的综合应用，考查计算能力，转化思想．
练习册系列答案
相关题目
已知椭圆的中心在原点，离心率e=
，且它的一个焦点与抛物线y2=-4x的焦点重合，则此椭圆方程为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知椭圆C：
+
=1(a＞b＞0)过点P(2，1)，离心率e=
，则椭圆的方程是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
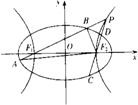如图，已知椭圆