题目内容
设等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() 为正整数),且满足
为正整数),且满足![]() 是
是![]() 与
与![]() 的等差中项;数列
的等差中项;数列![]() 满足
满足![]() 。
。
(1) 求数列![]() 的通项公式;
的通项公式;
(2) 试确定实数![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
(3) 当数列![]() 为等差数列时,对每个正整数
为等差数列时,对每个正整数![]() ,在
,在![]() 和
和![]() 之间插入
之间插入![]() 个2,得到一个新数列
个2,得到一个新数列![]() 。设
。设![]() 是数列
是数列![]() 的前
的前![]() 项和,试求满足
项和,试求满足![]() 的所有正整数
的所有正整数![]() 。
。
解: (1)由题意![]() ,则
,则![]() ,解得
,解得![]() 或
或![]()
因为![]() 为正整数,所以
为正整数,所以![]() ,
,
又![]() ,所以
,所以![]()
(2)当![]() 时,
时,![]() 得
得![]() ,
,
同理:![]() 时,得
时,得![]() ;
;![]() 时,得
时,得![]() ,
,
则由![]() ,得
,得![]() 而当
而当![]() 时,
时,![]() ,得
,得![]() 。
。
由![]() ,知此时数列
,知此时数列![]() 为等差数列。
为等差数列。
(3)由题意知,![]()
则当![]() 时,
时,![]() ,不合题意,舍去;
,不合题意,舍去;
当![]() 时,
时,![]() ,所以
,所以![]() 成立;
成立;
当![]() 时,若
时,若![]() ,则
,则![]() ,不合题意,舍去;从而
,不合题意,舍去;从而![]() 必是数列
必是数列![]() 中的某一项
中的某一项![]() ,则
,则![]()
![]()
![]()
又![]() ,所以
,所以![]()
![]() ,
,
即![]() ,所以
,所以![]()
因为![]() 为奇数,而
为奇数,而![]() 为偶数,所以上式无解。
为偶数,所以上式无解。
即当![]() 时,
时,![]()
综上所述,满足题意的正整数仅有![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
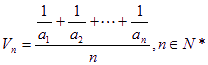 。
。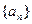 ,定义其倒均数是
,定义其倒均数是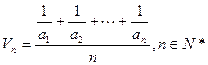 。
。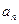 }的倒均数是
}的倒均数是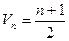 ,求数列{
,求数列{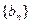 的首项为-1,公比为
的首项为-1,公比为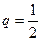 ,其倒数均为
,其倒数均为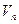 ,若存在正整数k,使
,若存在正整数k,使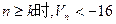 恒成立,试求k的最小值。
恒成立,试求k的最小值。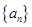 的首项为
的首项为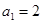 ,公比为
,公比为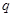 (
(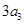 是
是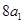 与
与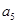 的等差中项;数列
的等差中项;数列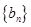 满足
满足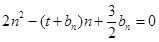 (
(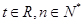 ).
).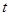 的值,使得数列
的值,使得数列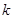 ,在
,在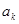 与
与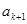 之间插入
之间插入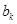 个2,得到一个新数列
个2,得到一个新数列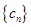 . 设
. 设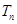 是数列
是数列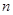 项和,试求满足
项和,试求满足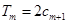 的所有正整数
的所有正整数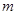 .
.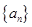 的首项为
的首项为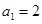 ,公比为
,公比为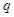 (
(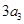 是
是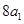 与
与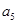 的等差中项;数列
的等差中项;数列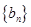 满足
满足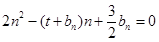 (
(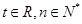 ).
).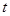 的值,使得数列
的值,使得数列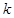 ,在
,在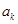 与
与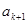 之间插入
之间插入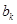 个2,得到一个新数列
个2,得到一个新数列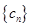 . 设
. 设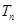 是数列
是数列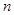 项和,试求满足
项和,试求满足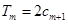 的所有正整数
的所有正整数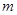 .
.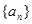 的首项为
的首项为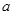 ,公比
,公比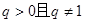 ,前
,前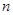 项和为
项和为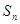
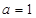 时,
时,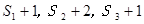 三数成等差数列,求数列
三数成等差数列,求数列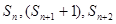 三数构成等差数列.
三数构成等差数列.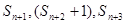 三数构成等差数列.
三数构成等差数列.